4.9 Vector-Valued Functions

4.9 Vector-Valued Functions

Hear me out: Our knowledge of parametric functions, planar motion, and vectors can be combined to represent planar motion in terms of vector-valued functions! 💰

➡️ Position Vector

The position of a particle moving in a two-dimensional plane can be represented by a vector-valued function, p(t) = x(t)i + y(t)j, where x(t) and y(t) are the coordinates of the particle at time t and i and j are the unit vectors in the x- and y-directions, respectively. 🧍

Alternatively, the position vector can also be represented in the form of p(t) = < x(t), y(t) >, where x(t) and y(t) are the components of the vector.

Source: Numeracy

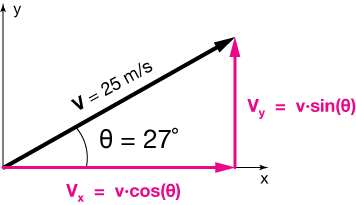
↗️ Velocity Vector

A vector-valued function, v(t) = < x(t), y(t) >, can be used to express the velocity of a particle moving in a two-dimensional plane at different times, t. The x and y components of the vector represent the horizontal and vertical velocities of the particle, respectively. 🚄

At any given time, t, the sign of x(t) indicates the direction of the horizontal velocity; a positive value indicates the particle is moving to the right ▶️ and a negative value indicates the particle is moving to the left. ◀️ Similarly, the sign of y(t) indicates the direction of the vertical velocity; a positive value indicates the particle is moving upwards 🔼 and a negative value indicates the particle is moving downwards. 🔽

Source: Xaktly