4.5 Implicitly Defined Functions

4.5 Implicitly Defined Functions

An equation involving two variables can implicitly describe one or more functions. The graph of the equation is the set of all solutions to the equation. The solutions are the coordinates (x, y) that make the equation true. 🧑‍🎨

📈 Graphing Equations Involving x and y

For example, the equation y = 2x + 1 can be graphed by plotting all the solutions (x, y) that make the equation true. To do this, we can substitute different values of x into the equation and solve for y. 🔁

The graph of the equation is a straight line that passes through the point (0, 1) and has a slope of 2. This line is the graph of the function y = 2x + 1. ↗️

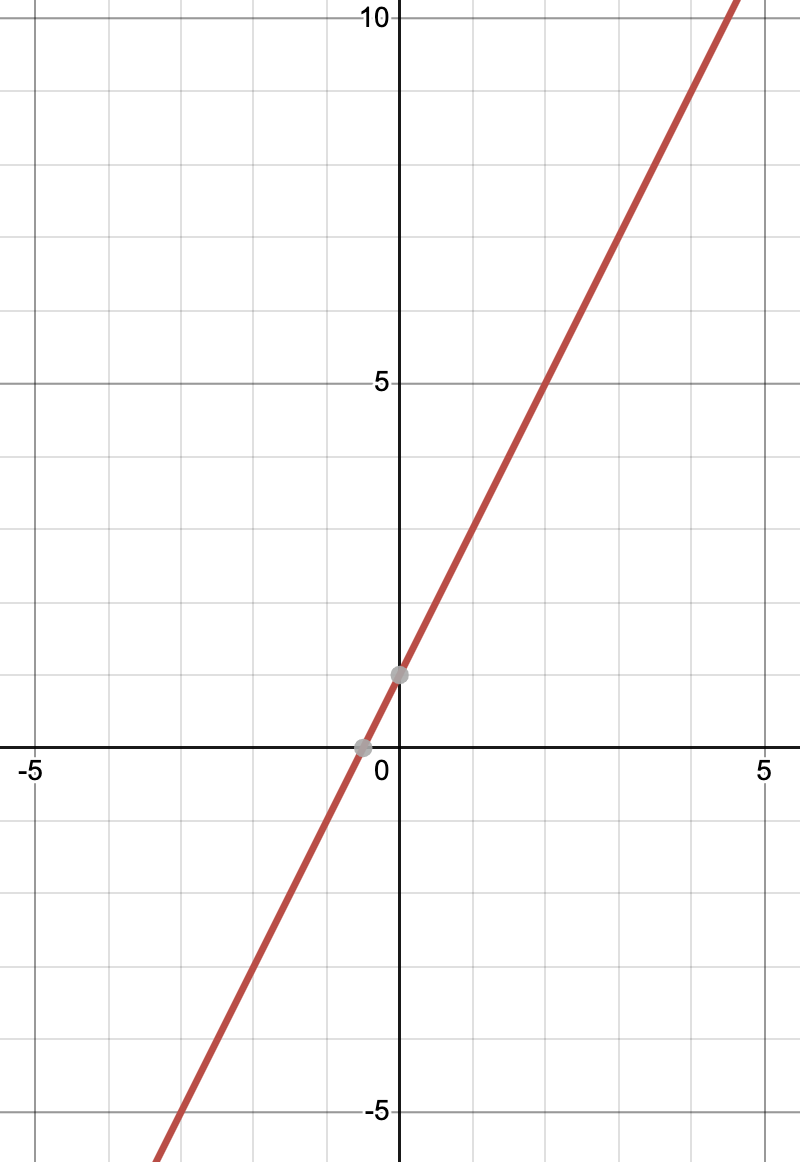
Source: Desmos

Solving for one of the variables in an equation involving two variables can define a function whose graph is a part or all of the graph of the equation.

For example, consider the equation x^2 + y^2 = 1. This equation describes the set of all points (x, y) that are equidistant from the origin, which is a circle with radius 1 centered at the origin. 🔘

Source: Desmos

If we solve for y, we get two functions, y = sqrt(1 - x^2) and y = -sqrt(1 - x^2). These two functions describe the upper and lower halves of the circle, respectively. We can graph these functions individually, and the combined graph of these two functions is the graph of the equation x^2 + y^2 = 1. 〽️

Similarly, if we solve for x, we get two functions x = sqrt(1 - y^2) and x = -sqrt(1 - y^2), which describe the left and right halves of the circle, respectively.

By solving for one of the variables we can also find the domain and range of the function that we get. It's important to notice that, in some cases, the domain of the function may be a restriction of the domain of the original equation, because some values of the variable that we solved for may not satisfy the original equation. 😮

📉 Relating Functions Involving x and y

The graph of an implicitly defined function is a set of all ordered pairs (x, y) that satisfy the equation. 👌 For any two ordered pairs that are close together on the graph, the ratio of the change in the two variables (i.e., the slope of the line connecting the two points) can be used to determine the relationship between the two variables.

For example, consider the equation x^2 + y^2 = 1. This equation describes the set of all points (x, y) that are equidistant from the origin, which is a circle with radius 1 centered at the origin. If we take two points that are close together on this circle, say (0.8, 0.6) and (0.9, 0.7), the ratio of the change in x and y is (0.9 - 0.8) / (0.7 - 0.6) = 1, the x and y values increase simultaneously.

It's important to note that the slope of the line connecting the two points is defined only when the line is not vertical or horizontal. In some cases, the slope can be infinite or undefined, which means that the line connecting the two points is vertical or horizontal, respectively! ♾️

Here’s another thing to consider:

When the rate of change of x with respect to y is zero, this means that the graph of the function is moving horizontally and the slope of the line connecting the two points is zero, indicating a horizontal interval. ↔️

Similarly, when the rate of change of y with respect to x is zero, this means that the graph of the function is moving vertically, and the slope of the line connecting the two points is undefined, indicating a vertical interval. ↕️

This can be visualized by the example of the equation x^2 + y^2 = 1, If we take two points (0.8, 0.6) and (0.8, 0.7) which are close together, the rate of change of x with respect to y is (0.8 - 0.8) / (0.7 - 0.6) = 0, indicating a horizontal interval. ✅