3.8 The Tangent Function

In the past few guides, we have been focusing on sinusoidal functions -- functions that look like the sine and cosine curves. In this guide, we will return to the unit circle to explore a third function that is not sinusoidal -- the tangent function. Then, we'll put together the ideas we learned about the transformation of sinusoidal functions and see how they apply to the non-sinusoidal function of tangent.

Constructing the Tangent Function from the Unit Circle

The tangent function, denoted by the symbol "tan", is a trigonometric function that is commonly used in mathematics and physics. It is defined as the ratio of the length of the side opposite a given angle in a right triangle to the length of the side adjacent to that angle. In other words, if a right triangle has an angle θ, with opposite side y and adjacent side x, the tangent of that angle is defined as tan(θ) = y/x.

Image courtesy of Softschools.

In order to understand and construct the graph of the tangent function using the unit circle, let's review the unit circle. The unit circle is a circle with a radius of 1 that is centered at the origin of a coordinate plane. The angle θ is measured counterclockwise from the positive x-axis in radians or degrees. To find the coordinates (x, y) of a point on the unit circle, we use the following equations:

x = cos(θ) and y = sin(θ)

Image courtesy of Remind.

The tangent of an angle is defined as y/x, and we related x and y to sine and cosine above, we can conclude that tan(θ) = sin(θ)/cos(θ). It is also important to realize that the tangent function represents the slope of the terminal ray, which is the line extending from the origin to the point on the unit circle. 

Like we did for sine and cosine, let's understand the behavior of the tangent function using patterns we find on the unit circle. As we move around the unit circle, the value of θ changes, and the coordinates (x, y) change. As a result, the equation f(θ) = tan(θ) traces out the graph of the tangent function. Starting at the 0-degree mark, and moving counterclockwise, we can see that the values for sin(θ)/cos(θ) are increasingly positive for the first quadrant. At θ = 𝛑/2, the value of sin(θ)/cos(θ) is 1/0, so the slope is--

Wait. We can't divide by 0!

This is where the behavior of the tangent function differs from sine and cosine. As you probably learned in algebra, the slope of a vertical line, such as the one created by the terminal ray at θ = 𝛑/2, is undefined. This means that at θ = 𝛑/2, there is a vertical asymptote in the graph of tangent. We'll come back to this in a moment. Let's continue analyzing the patterns we see in the unit circle.

Moving from θ = 𝛑/2 to θ = 𝛑, we see that the tangent values are negative, but increasing towards 0. In the third quadrant, the tangent values are positive (again?) because a negative divided by a negative becomes positive. At θ = 3𝛑/2, we have to divide -1 by 0, which is, again, not possible, so our slope is once again undefined. In the fourth quadrant, the values of tangent are once again negative and increasing.

Recall that the slope of the terminal ray is equal to the tangent of the angle. If you zoom out and look at the unit circle as a whole, you'll notice that the angles θ = 𝛑/6 and θ = 7𝛑/6 lie along the same line. This means that the two terminal rays pointing to these two angles have the same slope, and therefore, the tangent value of these two angles is the same. Based on this observation, the tangent function repeats every half-rotation around the unit circle, so it has a period of 𝛑, whereas the sine and cosine functions had a period of 2𝛑.

Now that we have learned the basic behavior of the tangent function, let's look at its graph to learn even more:

Image courtesy of Wolfram MathWorld.

This graph is certainly not a sinusoidal function, because it doesn't look like the sine wave. It has periodic asymptotes where the cosine of the angle θ is 0, which is at θ = 𝛑/2 + k𝛑, where k is an integer. This expression basically tells us that there is a vertical asymptote in the tangent function every time there is an integer coefficient multiplied to 𝛑/2, such as 3𝛑/2, 5𝛑/2, 7𝛑/2, and so on.

Another element of the tangent function we can notice from this graph is that it is always increasing. Even though the value of the tangent function resets to negative infinity every time there is an asymptote, the function is still increasing.

The reason that the range of the tangent function is negative infinity to infinity is because we cannot divide by 0. In the denominator, we can divide by 0.01, 0.001, 0.0001, and keep adding zeroes forever. This is why the graph goes to positive and negative infinity; because we can get infinitely close to zero in the denominator, but we cannot reach it and keep the function continuous.

Transformations of the Tangent Function

Now that we have explored the fundamentals of the tangent function, we can use those fundamentals to transform the tangent function and find the equations. 

The general equation for a tangent function is much the same as the equation for a sinusoidal function:

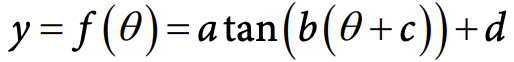
Image courtesy of CollegeBoard.

The tangent function has many of the same characteristics as a sinusoidal function, even though it is not a sinusoidal function. The breakdown of this equation is provided below. ⬇️

The amplitude of a function is a measure of how much the function oscillates above and below the center line or the x-axis. In this case, the amplitude of the tangent function is "a". The amplitude of the tangent function is the absolute value of "a" and determines the vertical dilation of the tangent function. If the value of "a" is negative, the function has been reflected over the x-axis.

The period of a function is the interval over which the function repeats itself. For the tangent function, the period is T = π/b. The smaller the value of "b", the wider the function gets and the greater the period is.

The phase shift of a function is a measure of how much the function is shifted horizontally. In this case, the phase shift of the tangent function is c. If c is positive, the graph is shifted to the right, and if c is negative, the graph is shifted to the left.

The vertical shift of a function is a measure of how much the function is shifted vertically. In this case, the vertical shift of the tangent function is d. If d is positive, the graph is shifted up, and if d is negative, the graph is shifted down.