3.9 Inverse Trigonometric Functions

By now, you are familiar with sine, cosine, and tangent, and how to graph these curves. However, there is so much more to trigonometry than just these three functions. We'll start by exploring the inverses of these functions -- arcsine, arccosine, and arctangent -- and how they relate to the more familiar trigonometric functions. Be sure to pay special attention to the domain and range restrictions placed on the original functions to get to the inverse functions.

But first, let's start with a quick review of what trigonometric functions are. Trigonometric functions are a set of functions that take an angle as an input and output a value that represents a ratio of the sides of a right triangle. The most commonly used trigonometric functions are sine, cosine, and tangent.

Inverses of Sine, Cosine, and Tangent

Now, let's move on to the inverse trigonometric functions. These functions are the inverses of the trigonometric functions we just discussed. In other words, they take a ratio of the sides of a right triangle as an input and output an angle. The inverse trigonometric functions are denoted with an "arc" in front of the function name, such as arcsine, arccosine, and arctangent.

The inverse trigonometric functions allow us to find the missing angle in a right triangle when we know the ratios of the sides. For example, if we know the ratio of the opposite side to the hypotenuse in a right triangle, we can use the arcsine function to find the angle opposite to that side. Similarly, if we know the ratio of the adjacent side to the hypotenuse, we can use the arccosine function to find the angle adjacent to that side. And if we know the ratio of the opposite side to the adjacent side, we can use the arctangent function to find the angle opposite to that side.

The shorthand forms of these functions are

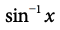
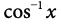
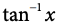
The graphs of the functions are shown below:

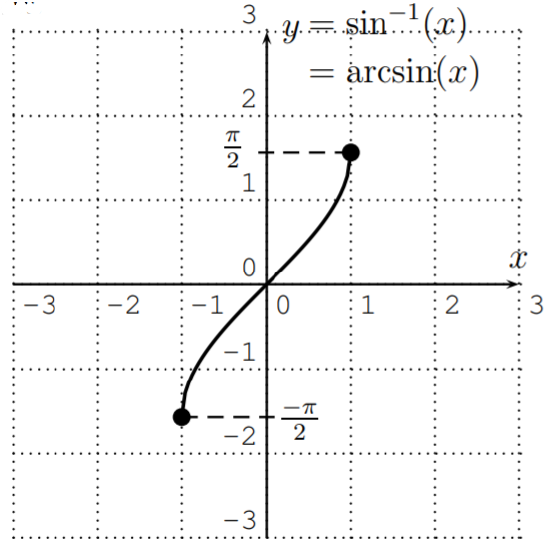
Graph of arcsine. Image courtesy of Math LibreTexts.

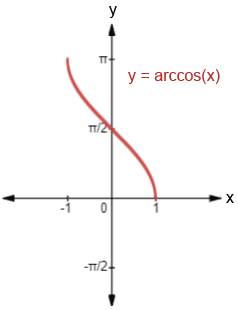
Graph of arccosine. Image courtesy of Math.net.

Image courtesy of Wiktionary.

As you can see, the graphs of arcsine and arccosine are finite, but the graph of arctangent goes on forever. This is due to the domain and range restrictions placed on the original sine, cosine, and tangent functions.

Restricting the Domain of the Sine Function

The sine function is periodic, which means that it repeats its values after a certain interval, known as the period. The period of the sine function is 360 degrees or 2𝛑 radians. This means that for any angle, there are an infinite number of angles that will give the same sine value. For example, the sine of 30 degrees is the same as the sine of 390 degrees, because 30 + 360 = 390. Similarly, the sine of 45 degrees is the same as the sine of 405 degrees, and so on.

When finding the inverse sine, we need to take the sine of an angle and find the angle that produced it. But since the sine function has a period of 2𝛑 radians, there are an infinite number of angles that can produce the same sine value, making it impossible to determine a unique angle. To ensure that we get a unique solution, we need to restrict the domain of the input value of sine to a specific range of angles.

The arcsine function, which is the inverse of the sine function, is defined over the range [-90,90] degrees or [-𝛑/2,𝛑/2] radians. This means that the output value for the arcsine function must be in this domain, so that we get a unique solution for the angle. To achieve this restricted range, we need to restrict the domain of the sine function to [-𝛑/2, 𝛑/2] radians since the domain of the original function becomes the range of the inverse function. The reason we denote the range in angle brackets is this is a closed interval, meaning -𝛑/2 and 𝛑/2 are included in the range and are valid outputs for the arcsine function.

Restricting the Domain of the Cosine Function

The cosine function, like the sine function, is periodic and has a period of 360 degrees or 2π radians. This means that for any angle, there are an infinite number of angles that will give the same cosine value. For example, the cosine of 60 degrees is the same as the cosine of 420 degrees (60+360=420), and the cosine of 75 degrees is the same as the cosine of 435 degrees, and so on.

Also like the sine function, there are an infinite number of angles that can produce the same cosine value, making it impossible to determine a unique angle. To ensure that we get a unique solution, we need to restrict the domain of the input value to a specific range of angles for the cosine function.

The arccosine function, which is the inverse of the cosine function, is defined over the range [0,180] degrees or [0,𝛑] radians. This means that the input value for the arccosine function must be in this range, so that we get a unique solution for the angle. Again, notice the square brackets denoting the closed interval for this function.

The range of the cosine function is [-1,1], which means that the output values of the cosine function are within this range. However, the cosine is non-negative for values in the range of [0,180] degrees or [0,𝛑] radians. Therefore, when we use the arccosine function, which is the inverse of the cosine function, we can restrict the domain of the input values to [0,180] degrees or [0,𝛑] radians to ensure that we get a unique solution.

Restricting the Range of the Tangent Function

The tangent function is defined over all real numbers except for multiples of 𝛑/2, and it is periodic with a period of 180 degrees or 𝛑 radians, which means that it repeats itself every 180 degrees or 𝛑 radians. The tangent function takes an angle as input and returns a value that represents the ratio of the opposite side to the adjacent side of a right triangle.

The range of the tangent function is all real numbers, which means that the output values of the tangent function can be any real number. However, the tangent function is not defined at certain angles, such as 90, 270, 450 and so on, which are known as the "singularities" or "undefined" values of the tangent function. Therefore, when we use the arctangent function, which is the inverse of the tangent function, we can restrict the domain of the input values to the tangent function to (-90,90) degrees or (-𝛑/2,𝛑/2) radians to ensure that we get a unique solution. This is because the arctangent function takes a real number as an input, and returns the angle that produced that value. Notice the open parentheses on this interval that show the arctangent function is defined on an open interval and will not output a value that is equal to -𝛑/2 or 𝛑/2, because the tangent value for these angles is undefined.

For example, if we want to find the angle that produced the tangent value of 1, we can use the arctangent function. The arctangent of 1 is 45 degrees, which is the angle that produced the tangent value of 1. If the input value for tangent is not in the range of (-90, 90) degrees or (-𝛑/2, 𝛑/2) radians, it might return an angle that is not unique, for example, 315 degrees, which also produces the same tangent value of 1. By restricting the domain, we can ensure that the output angle is unique and corresponds to a real-world angle.

Using the Unit Circle to Evaluate Inverse Trig Functions

The unit circle, as mentioned previously, is a very powerful tool that has a variety of uses. One of these uses is solving an inverse trigonometric function. The input of an inverse trig function (the value inside the parentheses) is the sine/cosine/tangent of the angle, so the question you are trying to answer is: what angle has a sine/cosine/tangent value of x?

Let's make this idea more concrete with an example: What does arctangent(1) evaluate to?

The question we are trying to answer here is: what angle has a tangent value of 1?

Image courtesy of Remind.

Looking at the unit circle, and trying out different angles within (-𝛑/2, 𝛑/2), we can see that the tangent value at 𝛑/4 is 1, so our answer is 𝛑/4 because that is the angle.

Practice Problems

1. What is the value of arcsin(-1/2)?

a) -30 degrees

b) -60 degrees

c) 30 degrees

d) 60 degrees

Answer: b) -60 degrees

2. What is the value of arccos(√2/2)?

a) 30 degrees

b) 45 degrees

c) 60 degrees

d) 90 degrees

Answer: d) 45 degrees

3. What is the value of arctan(√3)?

a) 45 degrees

b) 60 degrees

c) 90 degrees

d) 120 degrees

Answer: a) 60 degrees