2.10 Inverses of Exponential Functions

2.10 Inverses of Exponential Functions

We’ll now continue our conversation about logarithmic expressions, which mathematically translate into… logarithmic functions! Before we dive deeper into the nooks and crannies of such functions, let’s first connect the dots between them and a familiar face in this part of town: exponential functions. 📝

A logarithmic function can be defined as $f(x) = alog_b(x)$, where b is the base of the logarithm and a is the coefficient of the function. The base b must be greater than 0 and not equal to 1, and the coefficient a must not be 0. 🥴

The inverse relationship between the input and output values in exponential and logarithmic functions can be observed by comparing the general forms of these functions. The general form of an exponential function is $f(x) = ab^x$, where a is the coefficient and b is the base. As the input value x increases, the output value f(x) increases proportionately in equal-length intervals.

On the other hand, the general form of a logarithmic function is $f(x) = alog_b(x)$, where a is the coefficient and b is the base. As the output value f(x) increases, the input value x increases proportionately in equal-length intervals.

Coincidence? Definitely not! 😼

📖 A Story of Inverses

Exponential growth is characterized by output values changing multiplicatively as input values change additively, while logarithmic growth is characterized by output values changing additively as input values change multiplicatively. This is because in exponential functions, the input value is the exponent, and in logarithmic functions, the input value is the argument of the logarithm.

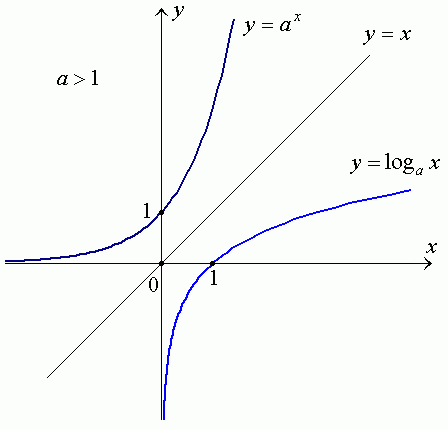
Source: GitHub

Reflections and the Identity Function h(x)

The graph of the logarithmic function $f(x) = log_b(x)$, where b > 0 and b ≠ 1, is a reflection of the graph of the exponential function $g(x) = b^x$, where b > 0 and b ≠ 1, over the graph of the identity function $h(x) = x$. This is due to the inverse relationship between logarithmic and exponential functions. 🪞

The exponential function $g(x) = b^x$ has a curve that increases rapidly as the x-value increases. The base b > 1, the greater the increase, while the base b < 1 the smaller the increase. The graph of the function g(x) has a vertical asymptote at x = 0 and has no horizontal asymptote.

On the other hand, the logarithmic function $f(x) = log_b(x)$ has a curve that increases slowly as the x-value increases. The base b > 1, the greater the slope of the curve, while the base b < 1 the smaller the slope of the curve. The graph of the function f(x) has a horizontal asymptote at y = 0 and has no vertical asymptote.

The identity function h(x) = x is a straight line with slope 1 and y-intercept 0. The graph of the function h(x) has no asymptotes. 🙅🏽

When the graphs of g(x) and f(x) are reflected over the graph of h(x), they become the same graph, but with the x and y coordinates switched. The resulting graph will have the shape of f(x) on one side of the identity line and the shape of g(x) on the other side of the identity line. This is why the graph of f(x) is a reflection of the graph of g(x) over the graph of h(x). 🔷

Applying the Relationship: Ordered Pairs

If (s, t) is an ordered pair of the exponential function $g(x) = b^x$, where b > 0 and b ≠ 1, then (t, s) is an ordered pair of the logarithmic function $f(x) = log_b(x)$, where b > 0 and b ≠ 1. This is because exponential and logarithmic functions are inverses of each other.

The exponential function $g(x) = b^x$ takes the input value x and raises the base b to the power of x, resulting in the output value t. If we have an ordered pair (s, t) where s is the input value and t is the output value, we can say that $t = b^s$.

On the other hand, the logarithmic function $f(x) = log_b(x)$ takes the input value x and finds the exponent to which the base b must be raised to equal x, resulting in the output value s. If we have an ordered pair (t, s) where t is the input value and s is the output value, we can say that $s = log_b(t)$. 🗣️

Since exponential functions and logarithmic functions are inverses of each other, we can say that if (s, t) is an ordered pair of the exponential function $g(x) = b^x$, then (t, s) is an ordered pair of the logarithmic function $f(x) = log_b(x)$. 🤩