2.3 Exponential Functions

2.3 Exponential Functions

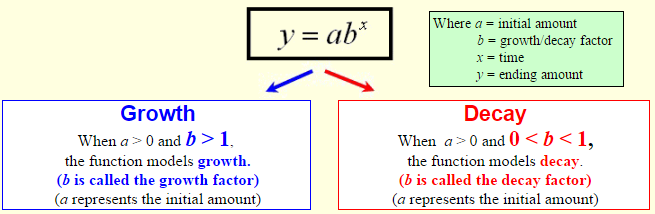
An exponential function is a function in which the variable, x, appears in the exponent, rather than in the base. The general form of an exponential function is $f(x) = ab^x$ , where a is the initial value, also known as the y-intercept, and b is the base, which is a positive number other than 1. ⭐

The behavior of an exponential function depends on the value of the base, b. When the base, b, is greater than 1 (b > 1), the exponential function demonstrates exponential growth. This means that as x increases, the value of the function, f(x), increases at an increasingly rapid rate. The larger the base, the faster the growth. 🆙

On the other hand, when the base, b, is between 0 and 1 (0 < b < 1), the exponential function demonstrates exponential decay. This means that as x increases, the value of the function, f(x), decreases at an increasingly rapid rate. The smaller the base, the faster the decay.

It's important to note that in both cases the initial value a must be greater than 0, otherwise the function would not be defined.

Source: A Plus Topper Domain****

The domain of an exponential function is all real numbers, which means that the function can be evaluated for any real number value of x. 🫂

When the natural numbers (1, 2, 3, 4, ...) are input values in an exponential function, the input value specifies the number of factors of the base to be applied to the function's initial value. For example, when x = 1, the function value is $f(1) = ab^1$, which is equal to ab. When x = 2, the function value is $f(2) = ab^2$, which is equal to $ab * b = b^2 * a$. In general, when x = n, the function value is $f(n) = ab^n$, which is equal to $b^n * a$, meaning that the base b is being multiplied by itself n times.

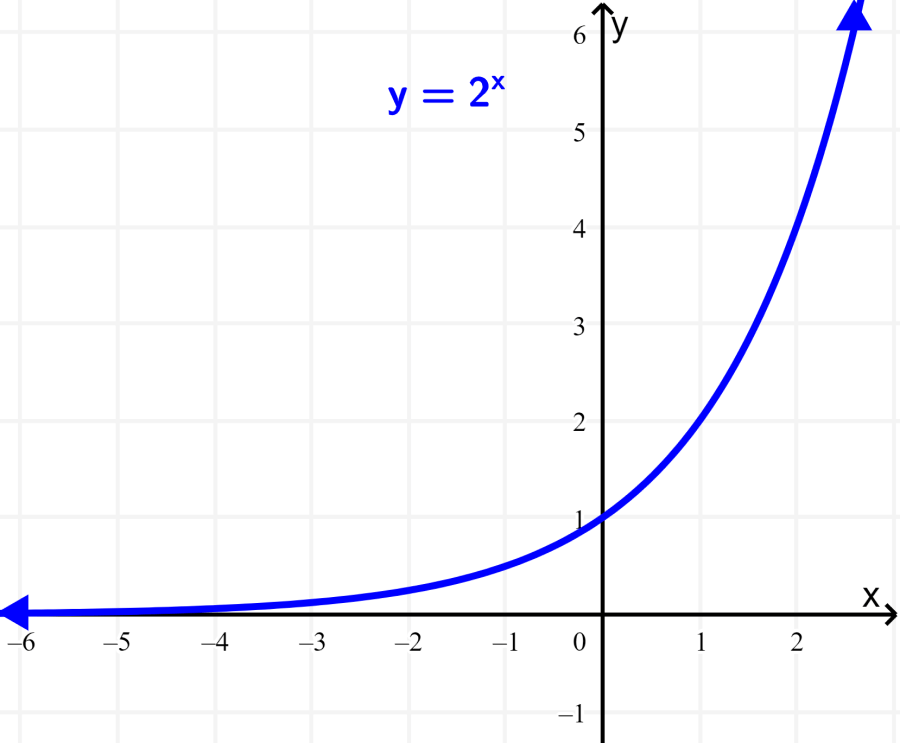
Source: Neurochispas

This idea can be used to model real-world situations that involve exponential growth or decay, such as compound interest, population growth, and radioactive decay. For example, if a population is growing at a rate of 5% per year, the population after n years will be $P*1.05^n$ , where P is the initial population. Here the base 1.05 represents the growth rate of 5% and the exponent represents the number of years. 🌆

↕️ Trends: Increasing vs. Decreasing, Concave Up vs. Down

Because the output values of exponential functions are proportional over equal-length input-value intervals, the graphs of exponential functions are always increasing or always decreasing.

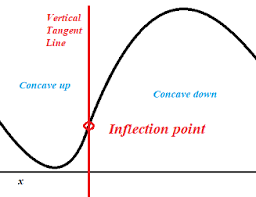
Depending on the value of the base, b, the function will have an upward or downward concavity. If the base, b, is greater than 1, the exponential function demonstrates exponential growth, and its graph is concave up. If the base, b, is between 0 and 1, the exponential function demonstrates exponential decay, and its graph is concave down.

Source: Lumen Learning

Consequently, exponential functions do not have extrema except on a closed interval, and their graphs do not have inflection points. The reason is that an inflection point occurs when a graph changes from concave up to concave down or vice versa, but since exponential functions are always concave up or always concave down, they do not have inflection points. 🙅🏽

An extrema is the highest or lowest value of a function, but exponential functions are always increasing or always decreasing and therefore, don't have extrema on an open interval.

Source: Statistics How To

Additive Transformations

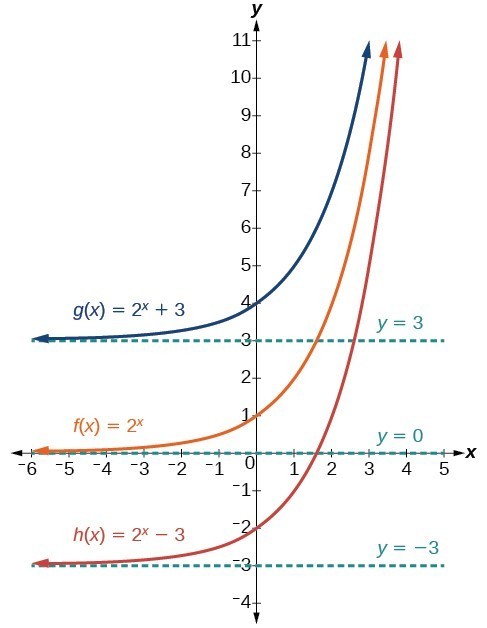
An additive transformation of a function f(x) is a function of the form g(x) = f(x) + k, where k is a constant. The additive transformation function g(x) shifts the graph of f(x) vertically by k units. ➕

If the values of the additive transformation function g(x) = f(x) + k of any function f are proportional over equal length input-value intervals, then f is exponential. This can be proven by observing that if the values of g(x) are proportional over equal length input-value intervals, then the graph of g(x) is exponential, and since g(x) = f(x) + k, the graph of f(x) is also exponential.

Exponential functions are functions that change proportionally over equal-length input-value intervals. This is, the ratio of the y-coordinates of two points on the graph of the function is the same for any two points. In other words, the graph of an exponential function is always increasing or always decreasing, and it's concave up if the base is greater than 1 or concave down if the base is between 0 and 1. 🫡

If we add a constant k to the function f(x) the graph will be shifted k units up or down but the shape of the graph will not change, this means that if the graph of g(x) = f(x) + k is an exponential function, then f(x) is also an exponential function.

Source: Lumen Learning

🛑 Limits

For an exponential function in general form, as the input values increase without bound, the output values will increase without bound or will get arbitrarily close to zero. If the base of the exponential function, b, is greater than 1, the output values of the function will increase without bound as x approaches positive infinity. The limit of the function as x approaches positive infinity is ∞. This means that as x gets larger and larger, the value of the function gets larger and larger without bound. 🪐

On the other hand, if the base of the exponential function, b, is between 0 and 1, the output values of the function will decrease without bound as x approaches positive infinity. The limit of the function as x approaches positive infinity is 0. This means that as x gets larger and larger, the value of the function gets closer and closer to zero. 0️⃣

The same behavior occurs when x approaches negative infinity. If the base of the exponential function, b, is greater than 1, the output values of the function will decrease without bound as x approaches negative infinity. The limit of the function as x approaches negative infinity is -∞. This means that as x gets more negative, the value of the function gets more negative without bound. 🔻

And if the base of the exponential function, b, is between 0 and 1, the output values of the function will increase without bound as x approaches negative infinity. The limit of the function as x approaches negative infinity is 0. This means that as x gets more negative, the value of the function gets closer and closer to zero.

Overall, this means that we have three possible scenarios for an exponential function in general form:

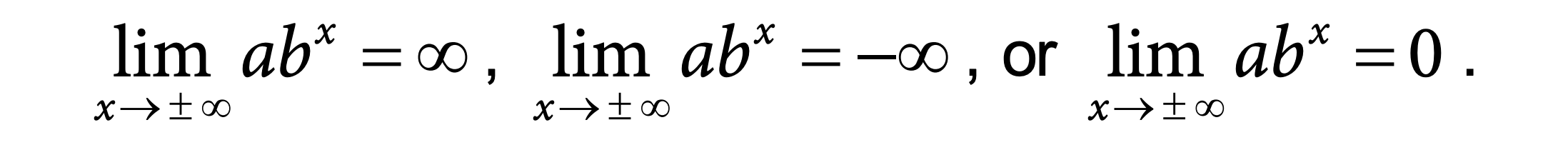
Source: Jed Q