<< Hide Menu
2.2 Change in Linear and Exponential Functions
1 min read•june 18, 2024
2.2 Change in Linear and Exponential Functions
In the previous section, you’ve noticed that arithmetic and geometric sequences are defined in graphs as discrete points—meaning, not connected by a smooth curve. Here, we’ll construct functions of real numbers that are actually comparable to said types of sequences. Yay for connecting the dots this time! 😃
👀 Arithmetic Sequence Lookalikes
A linear function is a function of the form , where is the y-intercept, the point at which the line crosses the y-axis, and is the slope, the rate of change of the function. The slope represents the steepness of the line and the direction in which the line is going up or down. A positive slope indicates that the line is going up, while a negative slope indicates that the line is going down. A slope of 0 indicates that the line is horizontal. ↕️
Recap time! An arithmetic sequence is a sequence of numbers where the difference between any two consecutive terms is always the same. It can be expressed as , where is the first term and is the common difference. The sequence can be generated by adding the common difference to the previous term.
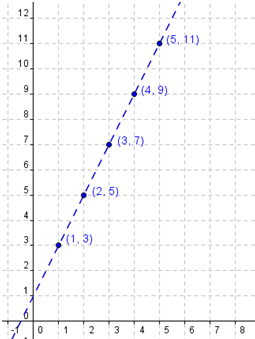
Image Courtesy of Math and Multimedia
Both linear functions and arithmetic sequences can be expressed as an initial value plus repeated addition of a constant rate of change. In linear functions, the initial value is represented by the y-intercept () and the constant rate of change is represented by the slope (). In arithmetic sequences, the initial value is represented by the first term () and the constant rate of change is represented by the common difference ().
For said reason, both can be used to model real-world situations that involve a constant rate of change, such as population growth, interest, and distance-time problems. ⏰
1️⃣ Similar Ways of Expression, Part 1
Similar to arithmetic sequences, linear functions can also be represented in terms of a known value and a constant rate of change. In arithmetic sequences, the known value is the kth term () and the constant rate of change is the common difference (). In linear functions, the known value is a point on the line (, ) and the constant rate of change is the slope ().
The point-slope form of a linear function, , and the explicit formula of an arithmetic sequence, , are similar in the sense that both allow us to find a value given a known value and a constant rate of change.
📐 Geometric Sequence Lookalikes
An exponential function is a function in which the variable, , appears in the exponent, rather than in the base. The general form of an exponential function is , where is the initial value and is the base, a positive number other than 1. This function represents the exponential growth or decay, depending on the value of b.
Recap time (…again)! A geometric sequence is a sequence of numbers where the ratio of any two consecutive terms is always the same. It can be expressed as , where is the first term and is the common ratio. The sequence can be generated by multiplying the previous term by the common ratio.
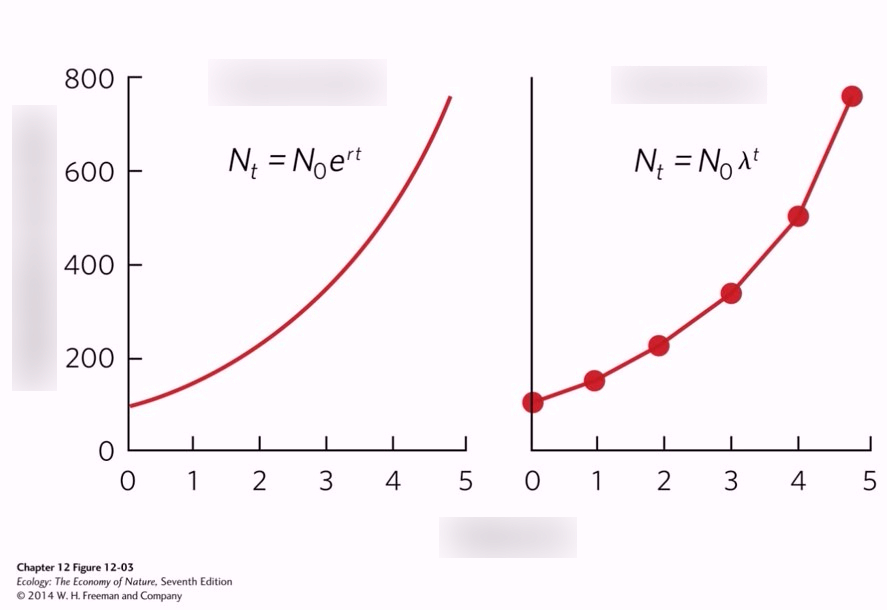
Image Courtesy of Quizlet, W. H. Freeman & Company
Both exponential functions and geometric sequences can be expressed as an initial value times repeated multiplication by a constant proportion. In exponential functions, the initial value is represented by a (y-intercept) and the constant proportion is represented by the base (). In geometric sequences, the initial value is represented by the first term () and the constant proportion is represented by the common ratio ().
For said reason, both can be used to model real-world situations that involve exponential growth or decay, such as compound interest, population growth, and radioactive decay. ☢️
2️⃣ Similar Ways of Expression, Part 2
Similar to geometric sequences, exponential functions can also be represented in terms of a known value and a constant ratio. In geometric sequences, the known value is the kth term () and the constant ratio is the common ratio (). In exponential functions, the known value is a point on the exponential function (, ) and the constant ratio is the ratio ().
The exponential form of an exponential function, , and the explicit formula of a geometric sequence, , are similar in the sense that both allow us to find a value given a known value and a constant ratio.
Again, similar looking formulas representing different concepts: functions =/= sequences! 🙅🏽
⚠️ Caveats of Sequence vs. Function: Domains!
Sequences and their corresponding functions may have different domains for several reasons. The domain of a sequence is typically the set of positive integers, while the domain of a function can be any set of numbers. For example, a sequence of the form , the domain is the set of positive integers, while the corresponding function , the domain is the set of real numbers.
In the image below, notice how the function (red line) includes values on the negative x-axis, while the sequence (dots) is limited to what comes after 0.
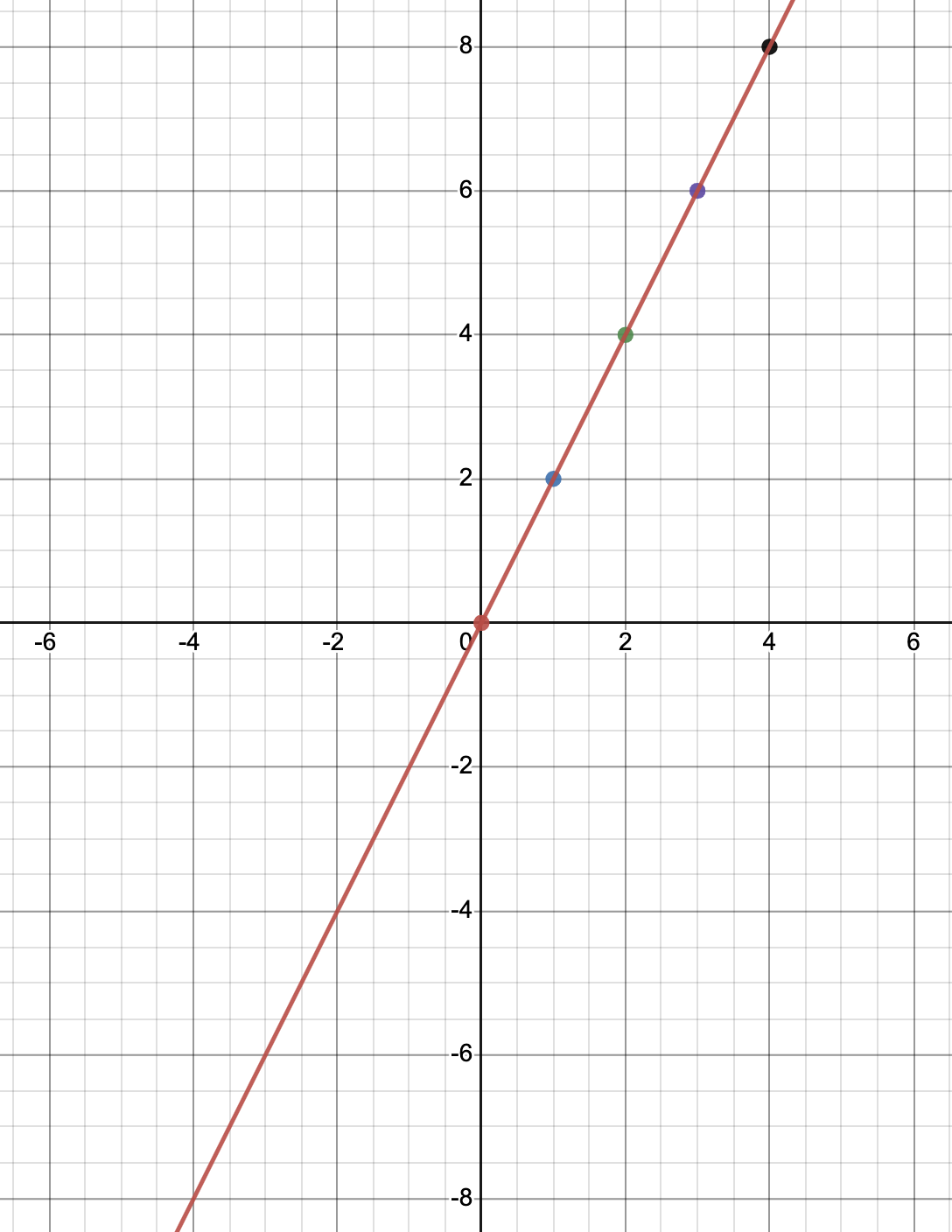
Image Courtesy of Jed Q on Desmos
Another reason is that some sequences are defined only for a specific range of values, while the corresponding function may be defined for a wider range of values. For example, a sequence of the form , the domain is the set of positive integers, while the corresponding function , the domain is the set of all real numbers.
A sequence can also be defined using a recursive formula, which is a formula that defines the nth term of a sequence in terms of the previous terms. In this case, the domain of the sequence may be restricted to the set of positive integers for which the formula is valid. A corresponding function, however, can be defined for a wider domain by using an explicit formula that relates the term of the sequence to the input variable. 🌎
Similarities and Differences
1️⃣ Over equal-length input-value intervals, if the output values of a function change…
- at a constant rate: the function is linear! This means that the slope of the function is constant, and the difference between the y-coordinates of two points on the graph of the function is the same for any two points.
- proportionally: the function is exponential! This means that the ratio of the y-coordinates of two points on the graph of the function is the same for any two points.
2️⃣ Linear functions of the form f(x) = b + mx and exponential functions of the form can both be expressed analytically in terms of an initial value and a constant involved with change.
- The initial value in a linear function is represented by the y-intercept (b), and the constant involved with change is represented by the slope (m).
- The initial value in an exponential function is represented by a, and the constant involved with change is represented by the base (b).
However, linear functions are based on addition, while exponential functions are based on multiplication.
3️⃣ Arithmetic sequences, linear functions, geometric sequences, and exponential functions all have the property that they can be determined by two distinct sequence or function values.
- In arithmetic sequences, two distinct sequence values are the first term and the common difference.
- In linear functions, two distinct function values are a point on the line and the slope.
- In geometric sequences, two distinct sequence values are the first term and the common ratio.
- In exponential functions, two distinct function values are a point on the function and the base.

© 2024 Fiveable Inc. All rights reserved.