1.12 Transformations of Functions

1.12 Transformations of Functions

Transformations! Now, let’s get familiar with additive and multiplicative transformations, which encapsulate translations, dilations, and reflections.

Additive Transformations (Translations)

An additive transformation of a function is a transformation that involves adding or subtracting a constant value to the function.

1️⃣ Vertical Translations

The function $g(x) = f(x) + k$ represents an additive transformation of the function f. In this case, the function f is being shifted vertically by k units. The value of k determines the magnitude and direction of the shift.

The result of this additive transformation is a vertical translation of the graph of f. A vertical translation is a transformation that involves moving the graph of a function up or down along the y-axis. In this case, the graph of f is being moved up or down by k units. ↕️

To visualize the effect of the additive transformation, we can plot the graphs of f and g on the same set of axes. The graph of f would appear in its original position, while the graph of g would be shifted horizontally by k units and vertically by k units.

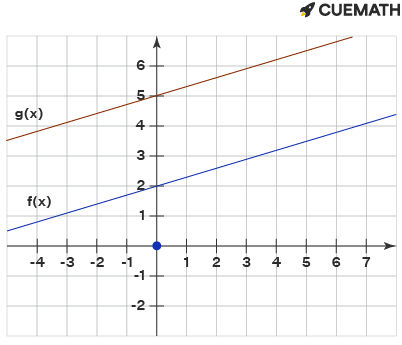
Image Courtesy of Cuemath

2️⃣ Horizontal Translations

The function $g(x) = f(x + h)$ also represents an additive transformation of the function f.

This time, the result of this additive transformation is a horizontal translation of the graph of f. A horizontal translation is a transformation that involves moving the graph of a function left or right along the x-axis. In this case, the graph of f is being moved to the left or right by h units, depending on the sign of h. ↔️

To visualize the effect of the additive transformation, we can plot the graphs of f and g on the same set of axes. The graph of f would appear in its original position, while the graph of g would be shifted horizontally by h units and vertically by 0 units.

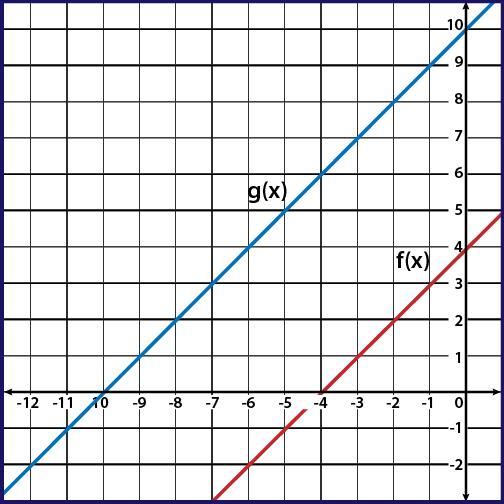
Image Courtesy of Quora

For both cases, it’s crucial to note that the shape of the graph of f remains unchanged by the additive transformation. Only its position on the coordinate plane is altered. 🚨 Therefore, if we know the graph of f, we can easily sketch the graph of g by applying the appropriate horizontal and vertical shifts.

🪞 Multiplicative Transformations (Dilations and Reflections)

A multiplicative transformation involves multiplying the function by a constant value.

1️⃣ Vertical Dilations

The function $g(x) = af(x)$, where a is a non-zero constant, represents a multiplicative transformation of the function f. In this case, the function f is being scaled vertically by a factor of |a|, which means the distance between the function and the x-axis is increased or decreased by a factor of |a|.

The result of this multiplicative transformation is a vertical dilation of the graph of f, a transformation that involves stretching or shrinking the graph of a function vertically.

• If $a > 1$, the dilation causes the graph of f to be stretched vertically, making the curve appear "taller." 🔼
• If $0 < a < 1$, the dilation causes the graph of f to be shrunk vertically, making the curve appear "shorter.” 🔽
• If $a < 0$, the transformation also involves a reflection over the x-axis, which means the graph of f is flipped over the x-axis. 🔁

To visualize the effect of the multiplicative transformation, we can plot the graphs of f and g on the same set of axes. The graph of f would appear in its original position, while the graph of g would be scaled vertically by a factor of |a|.

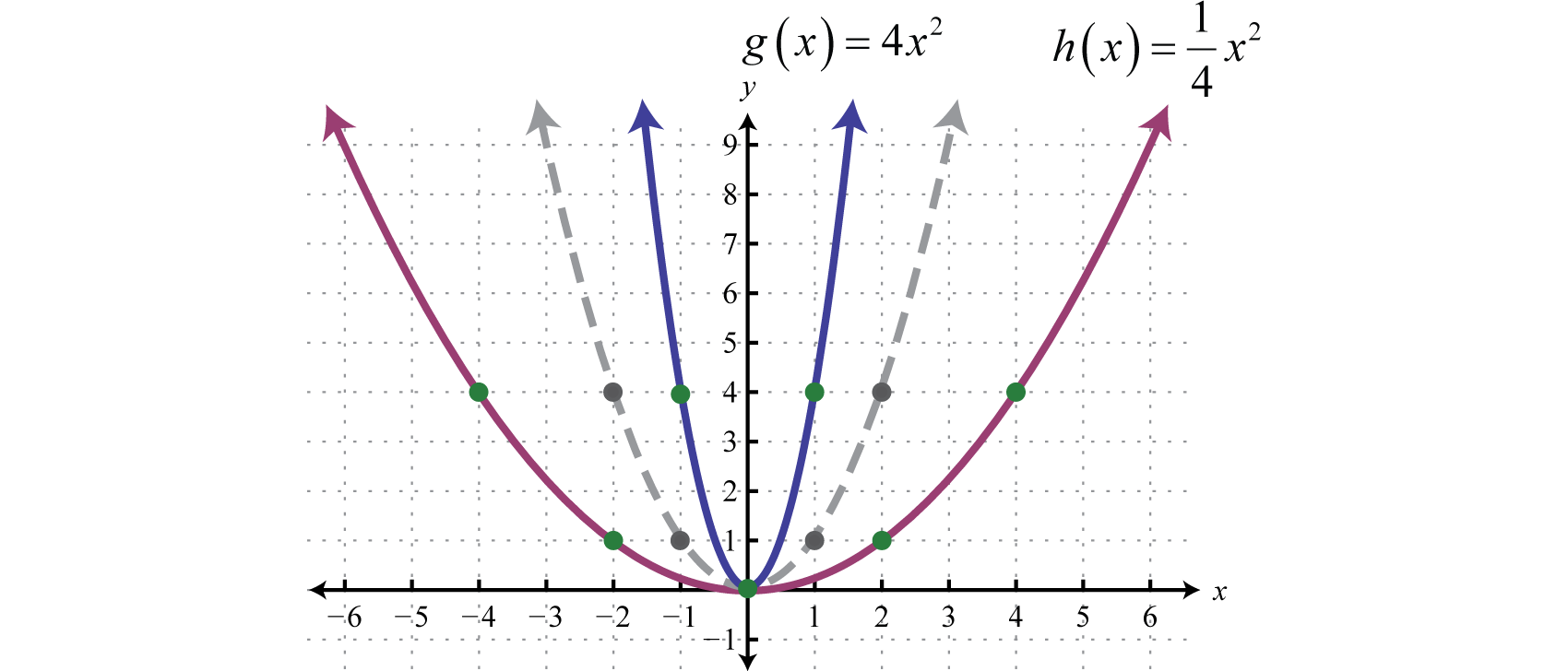
Image Courtesy of Github

2️⃣ Horizontal Dilations

The function $g(x) = f(bx)$, where b is a non-zero constant, also represents a multiplicative transformation of the function f.

In this case, the function f is being scaled horizontally by a factor of $|1/b|$, which means the distance between the function and the y-axis is increased or decreased by a factor of $|1/b|$.

The result of this multiplicative transformation is a horizontal dilation of the graph of f, a transformation that involves stretching or shrinking the graph of a function horizontally.

• If $|b| > 1$, the dilation causes the graph of f to be shrunk horizontally, making the curve appear "wider." ▶️
• If $0 < |b| < 1$, the dilation causes the graph of f to be stretched horizontally, making the curve appear "narrower." ◀️
• If $b < 0$, the transformation also involves a reflection over the y-axis, which means the graph of f is flipped over the y-axis. 🔁

To visualize the effect of the multiplicative transformation, we can plot the graphs of f and g on the same set of axes. The graph of f would appear in its original position, while the graph of g would be scaled horizontally by a factor of $|1/b|$.

Image Courtesy of Nagwa

For both cases, note that the shape of the graph of f remains unchanged by the multiplicative transformation. Only its size is altered. Therefore, if we know the graph of f, we can easily sketch the graph of g by applying the appropriate vertical dilation and reflection, if necessary.

Working with Transformations

Additive and multiplicative transformations can be combined to create more complex transformations of a function. When these transformations are combined, they result in a combination of horizontal and vertical translations and dilations. This means that the graph of the transformed function is shifted both horizontally and vertically and is also scaled horizontally and/or vertically. 😳

For example, consider the function $g(x) = a*f(bx + h) + k$, where a, b, h, and k are constants. This function is a combination of an additive and a multiplicative transformation of the function f. The function f is transformed horizontally by a factor of |1/b| and then horizontally translated by h units. It is also vertically scaled by a factor of a and then vertically translated by k units.

It is important to note that when a function is transformed, its domain and range may change. 😮 The domain of the transformed function may be restricted due to the nature of the transformations.

For example, if a function is reflected over the x-axis, its domain changes from all real numbers to all real numbers except zero. The range of the transformed function may also change due to the vertical scaling.

Image Courtesy of Lumen Learning