1.2 Rates of Change

1.2 Rates of Change

📐 Average Rates of Change: Speaking in Ratios

The concept of average rate of change is to measure the degree of change that occurs in a function over a given interval. The interval can be any section of the function's domain, and the average rate of change is calculated as the ratio of the difference between the output values at the endpoints of the interval to the difference between the corresponding input values. 📏

In simpler terms, the average rate of change is a measure of how fast or slow a function changes over a specific period. It is like measuring the slope of a straight line that connects two points on a graph of the function. However, instead of calculating the slope of a single point, the average rate of change considers the slope of the entire interval.

For instance, if we have a function f(x) defined over the interval [a, b], the average rate of change of f(x) over that interval would be $(f(b) - f(a))/(b - a)$. This formula calculates how much the output values of the function changed over the interval, relative to the change in input values.

By finding the average rate of change of a function, we can determine how much it is increasing or decreasing over an interval.

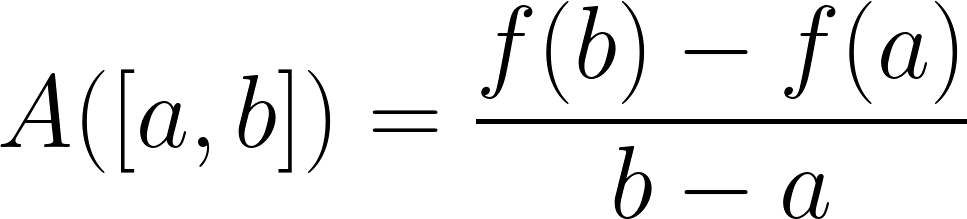
Image Courtesy of Inch Calculator

📈 Trends in Change

The rate of change of a function at a particular point refers to how quickly the output values of the function change when the input values change at that point. This rate of change is a measure of the function's slope at that point, indicating whether it is increasing, decreasing, or remaining constant. 😁

In simple terms, the rate of change at a point is like measuring how steep or flat a curve is at a particular point. If the curve is steeper, the rate of change is higher, and if it's flatter, the rate of change is lower.

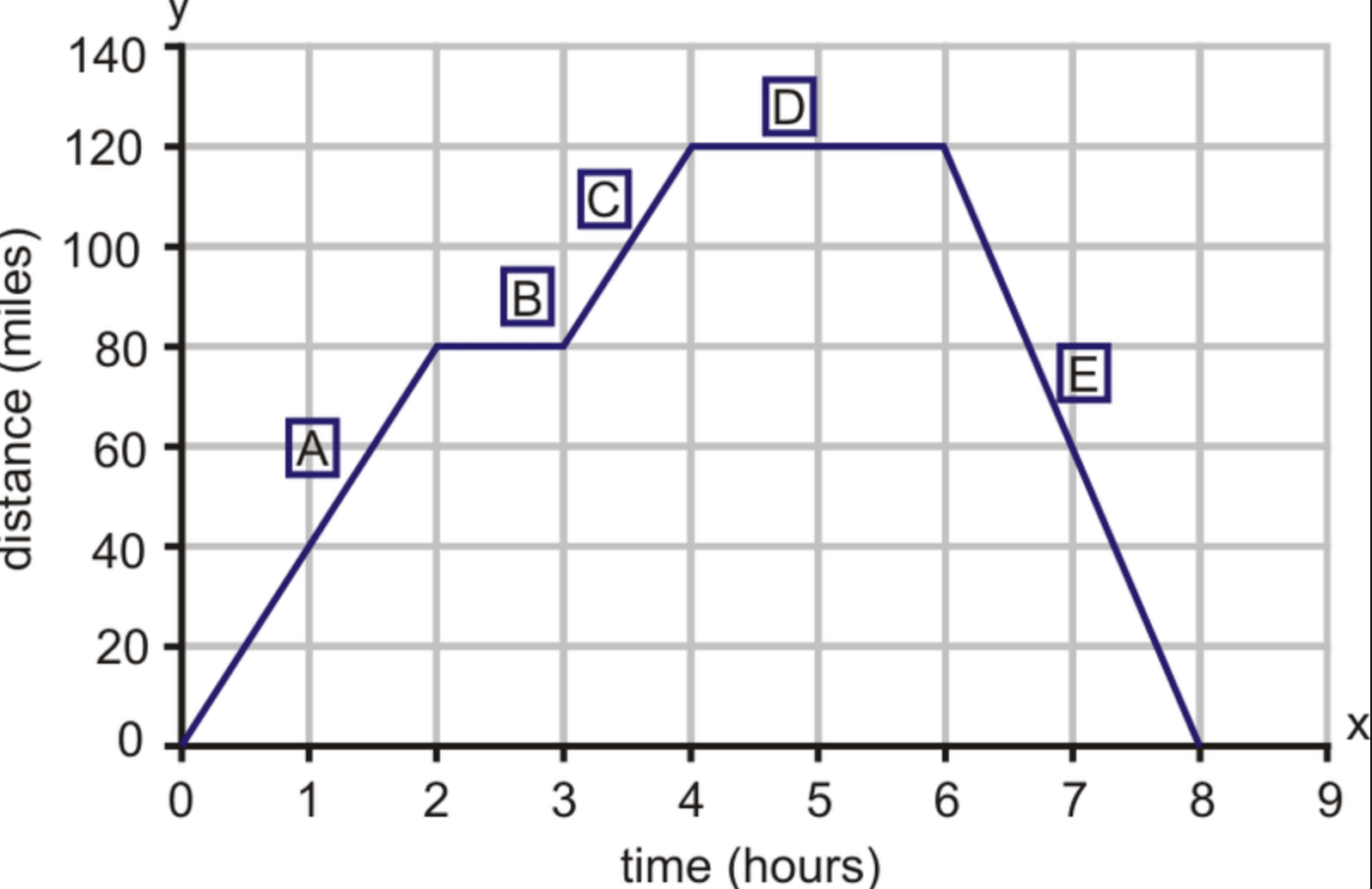
Image Courtesy of CK-12

When analyzing a function, it is often useful to compare the rates of change at two different points. To do so, we can use the average rate of change approximation over small intervals containing each point, provided that such values exist, as shown above.

Comparing these average rates of change can give us an idea of how quickly the function is changing at each point and how it's changing relative to other points. 🤓 

For example, if the average rate of change at one point is higher than the average rate of change at another point, then the function is changing more quickly at the first point than at the second point.

↕️ Positive and Negative Rates of Change

A positive rate of change means that as one quantity increases, the other quantity also increases. Similarly, if one quantity decreases, the other quantity also decreases.

For example, if we consider the speed of a car, a positive rate of change means that as the car accelerates, its speed increases. Conversely, if the car decelerates, its speed decreases.

On the other hand, a negative rate of change means that as one quantity increases, the other quantity decreases.

For instance, if we consider the height of an object as it falls to the ground, a negative rate of change means that as the object falls, its height decreases. This is because the height and the time are inversely related, with the height decreasing as the time increases.