1.11 Equivalent Representations of Polynomial and Rational Expressions

1.11 Equivalent Representations of Polynomial and Rational Expressions

Various Forms of Polynomial and Rational Expressions

Factored Form****

The factored form of a polynomial or rational function can provide valuable information about various aspects of the function's behavior. For example, the real zeros of the function can be easily determined from the factored form, which in turn can provide information about the function's x-intercepts and domain. ✖️

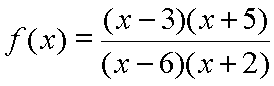
Source: Dalhousie University

Additionally, the factored form can reveal information about the presence of vertical or horizontal asymptotes, as well as any holes in the function. By analyzing the factors and their corresponding powers, one can determine the behavior of the function near these points. 😌

Furthermore, the factored form can also provide insight into the range of the function. By analyzing the behavior of the factors and their corresponding powers as the input values approach positive or negative infinity, one can determine the upper and lower bounds of the function's range. ↕️

Standard Form

The standard form of a polynomial or rational function can provide useful information about the behavior of the function as the input values approach positive or negative infinity, which is known as the end behavior of the function. 🧍

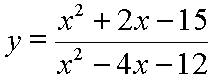
Source: Dalhousie University

For polynomials, the degree of the function and the sign of the leading coefficient can determine the end behavior.

• If the degree of the polynomial is even and the leading coefficient is positive, the function approaches positive infinity as the input values approach positive or negative infinity. 👆🏽
• If the degree is even and the leading coefficient is negative, the function approaches negative infinity as the input values approach positive or negative infinity. 👇🏽
• For odd-degree polynomials, the end behavior is determined by the sign of the leading coefficient, with positive leading coefficients approaching positive infinity and negative leading coefficients approaching negative infinity. 🧐

Similarly, for rational functions, the end behavior can be determined by comparing the degrees of the numerator and denominator. 😁

• If the degree of the numerator is less than the degree of the denominator, the function approaches zero as the input values approach positive or negative infinity.
• If the degrees are equal, the function approaches a horizontal asymptote determined by the ratio of the leading coefficients.
• If the degree of the numerator is greater than the degree of the denominator, the function approaches positive or negative infinity, depending on the signs of the leading coefficients.

Analyzing different analytic representations of the same polynomial or rational function can provide valuable information that can be used to answer questions in context.

Moreover, graphing the polynomial or rational function can provide a visual representation of its behavior and help to answer questions in context. The graph can reveal information about the function's behavior at specific input values, such as maxima, minima, and points of inflection. It can also provide insight into the shape and symmetry of the function, which can be important in understanding the function's behavior in specific contexts. 🤩

Quotients of Two Polynomial Functions

Polynomial long division is a very useful technique used to divide one polynomial function by another. The process is similar to numerical long division, but instead of working with numbers, we work with polynomials! ➗

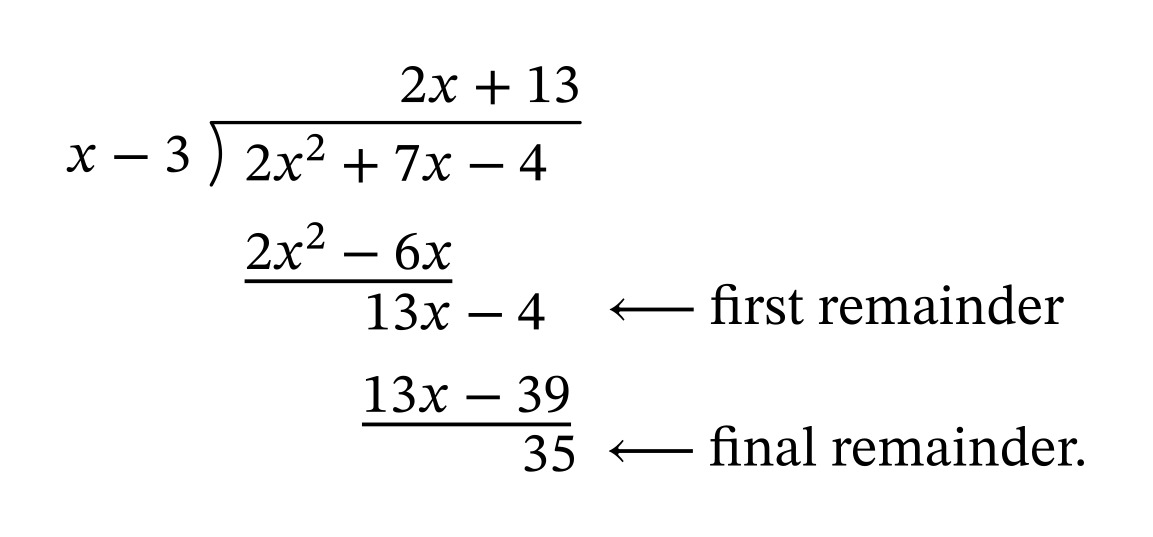
Source: Nagwa

To perform polynomial long division, we divide the highest degree term of the dividend (the polynomial being divided) by the highest degree term of the divisor (the polynomial doing the dividing). This gives us the first term of the quotient. 🥇

We then multiply the divisor by this term and subtract the result from the dividend. The resulting polynomial is then used as the new dividend, and we repeat the process until the degree of the new dividend is less than the degree of the divisor.

At this point, we have our final quotient and remainder, which can be written as f(x) = g(x)q(x) + r(x), where q(x) is the quotient and r(x) is the remainder. The degree of the remainder is always less than the degree of the divisor, which is an important property of polynomial long division.

Source: Quora

The result of polynomial long division is helpful in finding equations of slant asymptotes for graphs of rational functions. 👍🏼

The Binomial Theorem

The binomial theorem is a powerful tool that allows us to easily expand expressions of the form (a + b)^n, aka repeated products of binomials. It works by utilizing the entries in a single row of Pascal's Triangle, a triangular arrangement of numbers in which each number is the sum of the two numbers above it. 📐

Source: Online Math Learning

By using the binomial theorem, we can quickly and easily expand polynomial functions of the form p(x) = (x + c)^n, where c is a constant and n is a non-negative integer. This can be especially useful in simplifying complex polynomial expressions and finding zeros of polynomial functions. 🤓

The binomial theorem states that (a + b)^n can be expanded as the sum of n + 1 terms, each of which is a binomial coefficient times a power of a and a power of b. The binomial coefficients are the numbers in the nth row of Pascal's Triangle, and they can be determined using the formula (n choose k), where n is the power of the binomial and k is the index of the term in the expansion.

Expanding polynomial functions of the form p(x) = (x + c)^n using the binomial theorem can also reveal important properties of the function, such as the degree of the polynomial and the location of any vertical or horizontal asymptotes. Check out the example below ⬇️

Source: Maths at Home