1.6 Marginal Analysis and Consumer Choice

Introduction

Marginal analysis allows us to explain how consumers make choices about what goods and services to purchase. As consumers, we want to maximize our satisfaction, which is known as utility maximization. In economics, utility is defined as satisfaction. As a reminder, marginal utility is essentially the same thing as marginal benefit. We'll be adding onto what we talked about in Unit 1.5 by asking the question of maximizing utility between two goods. Essentially we'll asking what quantities of both goods maximizes utility. This involves understanding choices and costs, and is a problem you solve in your head every day at the grocery store. A motivating example may be if you are buying bread and chicken. You only have so much money, so you have to find what bundle of chicken and bread maximizes your utility. These problems are common in AP FRQs. 

Rules for Utility Maximization

Here are some assumptions we'll make to solve this problem:

• The consumer will spend all of their income.
• The consumer will buy only two goods. You can theoretically solve for 3+ goods, but that involves multivariable calculus, so you won't ever have to even get near that for this course, but if you're interested, feel free to google around! This article is a great place to start.
• When choosing which good to buy next, the consumer will always choose the good with the greatest MU/P (Marginal Utility per dollar, think of this like "bang for your buck").
• When a consumer stops buying, the MU/P of the last unit of each good should equal each other.

Steps for working these problems

• If you are given total utility (TU), you must first calculate marginal utility (MU). To calculate the MU, you subtract the TU going from one unit to another. Sometimes, the problems will give you marginal utility (MU); in this case, you can jump right to the second step!
• Once you have marginal utility (MU), calculate marginal utility per dollar (MU/P). This is done by dividing your marginal utility (MU) by the price of the product.
• Once you have calculated all these values, the consumer will look to buy the good that has the greatest MU/P first. Then, subtract the cost of that good from your budget.
• You continue this process until you have spent all of your budget.

Why Is Utility Maximized When MU1/P1 = MU2/P2? 

While a mathematical derivation of this principle requires some more advanced math and is not necessary for this course, we can intuitively understand why this principle exists using similar logic to how we explained MB = MC.

First, let's understand why we're looking at MU/P (marginal utility per dollar) and not just MU. This is because each good has a different price, so we need to look at each utility and cost in the same terms. This can also be thought of as "bang for your buck," since you spend some money for the benefit. If you get 10 utils as MU1 and MU2, but P1 is $100 and P2 is$10, you get a significantly higher bang for your buck (or MU per dollar) from good 2.

Using similar logic to MB = MC, it can be seen that utility is maximized when MU1/P1 = MU2/P2. When MU1/P1 > MU2/P2, we should consume more of good 1, since we get a bigger bang for our buck, and vice versa. Because of diminishing marginal utility, we will eventually settle where MU1/P1 = MU2/P2.

Sample Questions

Question 1

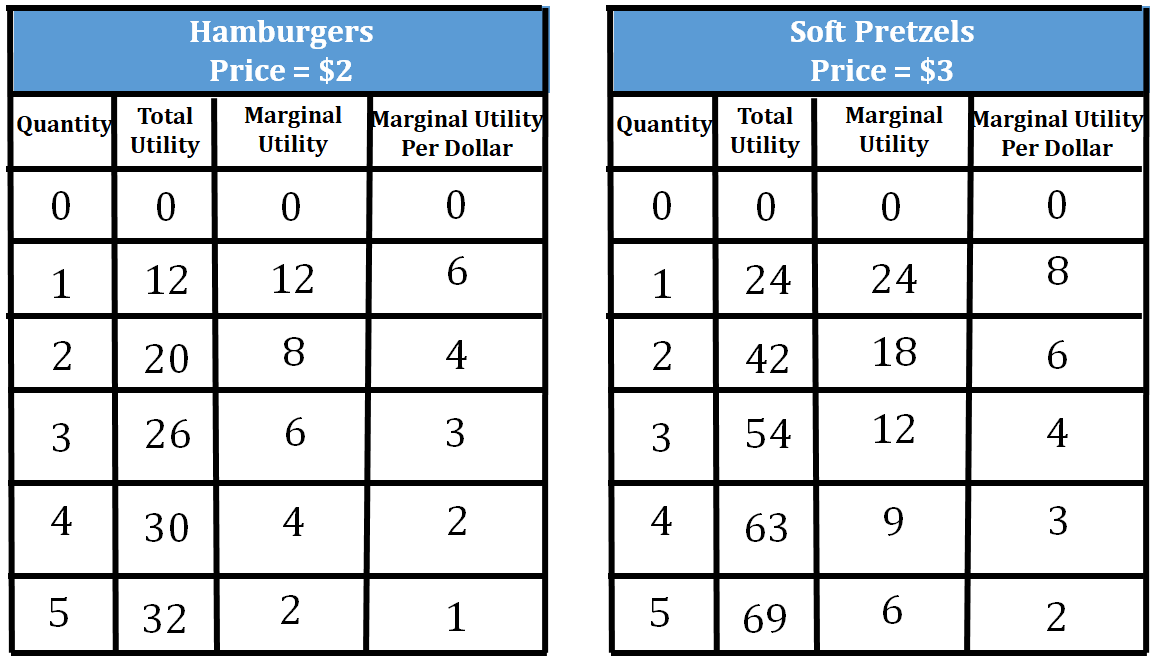
If the budget given to Sam at the local county fair for food is $18, what would be the combination of hamburgers and soft pretzels that would maximize his utility?

Answer 

3 hamburgers 4 soft pretzels

Explanation

1. He would first buy ONE soft pretzel because the MU/P of 1 soft pretzel is 8 and the MU/P of one hamburger is 6. He will be left over with $15.
2. Next, he will buy a SECOND soft pretzel (MU/P = 6) and a FIRST hamburger (MU/P = 6). He will have $10 at this point.
3. Then, he will buy a SECOND hamburger (MU/P = 4) and a THIRD soft pretzel (MU/P = 4). He will end up with $5 after this.
4. Finally, to use the last of his budget, he would buy his THIRD hamburger (MU/P = 3) and the FOURTH soft pretzel (MU/P = 3)

The ideal combination would be 3 hamburgers and 4 soft pretzels. MU/P of 3 hamburgers = MU/P of 4 soft pretzels (3 = 3), while still staying in budget.

Question 2

If Heather has a budget of $21 to purchase packs of pencils and composition books for the upcoming school year. What would be the combination of packs of pencils and composition books she could purchase in order to maximize her utility?

Answer

3 packs of pencils 3 composition books

Explanation

1. She would first buy ONE composition book because the MU/P of 1 composition book is 7 and the MU/P of one pack of pencils is 6. She would be left with $17.
2. Next, she will buy her FIRST pack of pencils (MU/P = 6) instead of a second composition book (MU/P = 5). Since 6 is greater than 5, this is the best decision. She will have $14 left over at this point.
3. She will then purchase a SECOND pack of pencils (MU/P = 5) and a SECOND composition book (MU/P = 5). Since the MU/P for both these items is 5, she will purchase both items. She will still have $7 remaining.
4. Finally, she will purchase both a THIRD pack of pencils (MU/P = 4) and a THIRD composition book (MU/P = 4).

The ideal combination would be 3 pack of pencils and 3 composition books. MU/P of 3 packs of pencils = MU/P of 3 composition books (4 = 4), while staying in budget.

Question 3

On the AP Microeconomics exam, they may just give you the MU and price of each good and ask if it is the ideal combination. Here is an example:

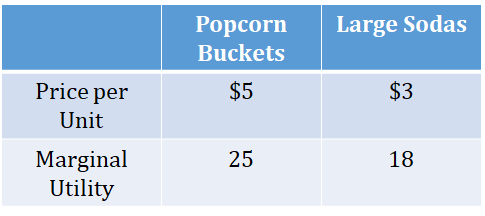
The table below shows the per-unit prices and marginal utility for the last unit of popcorn buckets and large sodas that Donna purchased. Donna spent all of her allocated budget on buckets of popcorn and large sodas at the movies. To maximize her utility, Donna should have purchased:

(A) more buckets of popcorn and fewer large sodas

(B) fewer buckets of popcorn and more large sodas

(C) fewer of both goods

(D) equal amounts of both goods

(E) more of both goods

Answer

Choice B 

Explanation

Donna should purchase more large sodas and less popcorn buckets because the MU/P of large sodas is greater than the MU/P of buckets of popcorn (MU/P of large sodas is 18/3, which is 6, and the MU/P of buckets of popcorn is 25/5, which is 5). Since 6 > 5, large soda has a greater utility-per-dollar value than popcorn buckets.

The rule of thumb is: if the MU/P for the two goods are not equal, then you buy more of the higher value good and less of the lower value good.

Law of Diminishing Marginal Utility

The Law of Diminishing Marginal Utility essentially says that as you consume more and more of a good or service, the additional satisfaction you get from that product decreases more and more. Let's say you were eating cake. For the first slice you eat, you get a lot of utility or satisfaction. For the second slice you eat, you get about the same amount of utility. But as you eat the third, fourth, and fifth slices, you start to gain less satisfaction. By the sixth slice, the marginal utility may actually become negative (which means that your total utility is actually decreasing) because you feel sick from all that sugar.