1.1 Moles and Molar Mass

Moles and molar mass are essential key concepts to understand when studying chemistry since they will allow you to accurately calculate and interpret chemical quantities and conversions. Think about it this way: how do scientists perform laboratory work when it's nearly impossible to count the atoms they are working with🤔?

The Atom

First, imagine an atom, the basic unit of matter that makes up all elements. Well, most likely you can't even begin to grasp how small an atom even is⚛️. An atom is made up of three types of subatomic particles: protons, neutrons, and electrons.

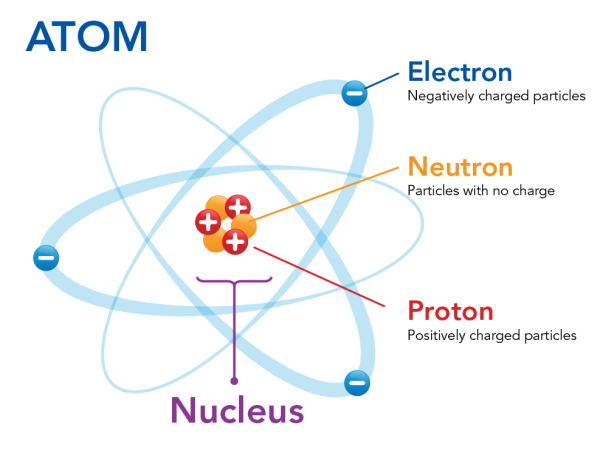
Image Courtesy of Let's Talk Science. There are different models of an atom, but the above is an example of where subatomic particles may exist.

Protons and neutrons are located in the nucleus at the center of the atom, while electrons orbit the nucleus. The nucleus is a small, dense core at the center of the atom. Since protons have a + charge and neutrons are neutral, the nucleus is very overall very positive. Electrons, orbiting the nucleus, have a negative charge and counteract the positive center of the atom.

We'll discuss the atom in more depth later in this unit, but it is important to understand how small it is. This is where the concept of a mole emerged. 

What is a mole?

Since scientists cannot count the tiny particles and atoms they are experimenting with, there must be a correlation between the mass of substances involved in a chemical reaction and the number of particles undergoing change. This is exactly what the mole is!

A mole relates the mass of an element to the number of particles there are. The analogy between a mole and a dozen of eggs can be helpful in understanding the concept of a mole in chemistry. Just as a dozen is a unit of measurement for eggs, a mole is a unit of measurement for particles in a substance.

🎥 Watch Dylan Black go over what a mole is and how to apply it to conversions, molar masses, and percent composition.

Molar Mass of a Substance

What is molar mass? 

The molar mass of a substance is the number of grams there are in a mole. Hence, the units for molar mass are grams/mole (or g/mol). Molar mass is important because it allows us to convert between mass, moles, and the number of particles.

Finding the molar mass of an element or compound is not as hard as it might seem: the only things that you need to know are which elements are involved and how many of them are present. This is also where the periodic table of elements comes in. 

On the periodic table, each element is represented by a one-to-two-letter abbreviation. You can also see a number above and below each chemical symbol. The number above, going chronologically across the periodic table, is the atomic number. The atomic number represents the number of protons in the nucleus of an atom of that element. The number below each symbol is the element's atomic mass. This is the mass of one atom of the element in atomic mass units (amu). 

👉 Cool Interactive Periodic Table

This is the periodic table that will be provided for you during the AP Chemistry Exam. You may access it online here. 

How do I calculate molar mass?

Let's first calculate the molar mass of water (H2O). First, break down the compound of interest. In one molecule of water, we have 2 atoms of hydrogen and 1 atom of oxygen.

From here, we have to take a look at the periodic table and find out how much each atom of hydrogen and oxygen weighs. This is where we have to take a look at the atomic mass of an element. The atomic mass of hydrogen is 1.008 g/mol and the atomic mass of oxygen is 16.00 g/mol. Since there are two atoms of hydrogen and one atom of oxygen in water, we must multiply 1.008 by 2, and then add that product to 16.00. This is how you can calculate the molar mass of water: 18.02 g/mol! 🥳

Calculating Molar Mass: Carbon Dioxide

Let's say we now have the compound CO2 or carbon dioxide. Remember, to calculate the molar mass, you simply have to multiply the atomic mass of each specific element by its subscript, and then add it all together. 

Carbon has a subscript of 1 and an atomic mass of 12.01 grams according to the periodic table. Oxygen has a subscript of 2 in this compound and has an atomic mass of 15.99 grams. Always multiply the subscript by the atomic mass of the element:

Carbon: 1 x 12.01 = 12.01 g

Oxygen: 2 x 16.00 = 32.00 g

Finally, we add 32.00 grams to 12.01 grams to get 44.01 grams. Therefore, CO2 has a molar mass of 44.01 grams per mole.

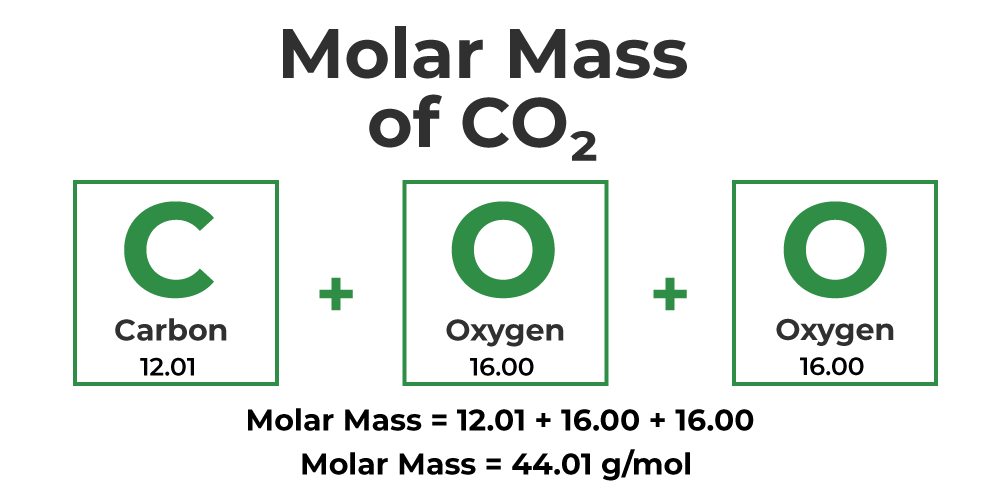
Image Courtesy of GeeksforGeeks

Avogadro's Number 

Remember the analogy between a mole and a dozen? Just as a dozen eggs contains 12 eggs, a mole of a substance contains 6.022 x 10^23 particles. This very large number is Avogadro's number. To put this into perspective, a mole of hockey pucks would be equal to the mass of the Moon. In chemistry, this number is relevant when converting from grams to moles to atoms.

Dimensional Analysis

One of the most fundamental takeaways from this unit is dimensional analysis, and you'll be using it throughout the rest of this course! This is a technique used to convert between different units of measurement, and you've probably implicitly done it before.

For example, you can use dimensional analysis to convert from miles per hour to meters per second, or from inches to centimeters.

Dimensional analysis is going to be so useful throughout this course, especially when you forgot a formula that is essential to solving the question!

When doing dimensional analysis, you start by identifying the units you are trying to convert from and the units you want to convert to. Then, you write down the conversion factor that will allow you to make the conversion. Finally, you multiply the value you are trying to convert by the conversion factor to get the final result.

A conversion factor is a ratio of equivalent units that can be used to convert one set of physical units to another. These are usually known facts, such as 1 foot = 12 inches and 1 meter = 3.28 feet.

Dimensional Analysis with Moles and Molar Mass

Now that we've discussed the fundamental concepts of moles and molar mass, let's try converting a sample of 50.0 grams of CO2 between units.

CO2 - Converting from Grams to Moles 

Since we know we have to convert from grams to moles, we have to figure out what conversion factor can help us do this. First, put the number that is given to you in the problem, which in this case, is 50.0 grams of CO2. 

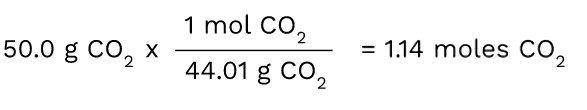
Then, you want to multiply 50.0 by the molar mass in order to convert it to the moles of CO2. The unit that you have (grams of CO2) should always be on the bottom of the next ratio in order for the units to cancel out. Here, the grams of CO2 cancel out and you are left with a measurement in moles. 

Tip: It is good to memorize that moles = grams/molar mass. The conversion factor in this problem is actually using this concept since you are ultimately dividing the number of grams you have by the molar mass to get the number of moles.

CO2 - Converting from Moles to Atoms

Now let's convert 1.14 moles of CO2 into atoms using Avogadro's number.

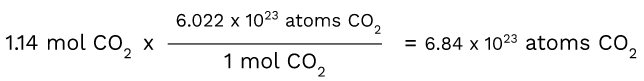
Here, you are once again taking the number that you have and putting it first. Then, you are putting the unit of measurement that you want over the unit of measurement that you have, making that step the conversion factor. This enables the moles of CO2 to cancel out, leaving you with just 6.84x10^23 atoms of CO2.

Keep in mind that the concept of Avogadro's number serves as the conversion factor when going from moles to atoms.

CO2 - Finding the number of atoms of C

Since the subscript on Carbon is 1, the number of atoms of CO2 is equivalent to the number of carbon atoms in CO2. There is nothing to multiply by because of this 1-to-1 ratio; therefore the number of carbon atoms in this 50.0g sample of CO2 is 6.84x10^23.

CO2 - Finding the number of atoms of O

Unlike carbon, oxygen has a subscript of 2. This makes the ratio of CO2 atoms to oxygen atoms 1:2. Therefore, we have to use dimensional analysis again: 

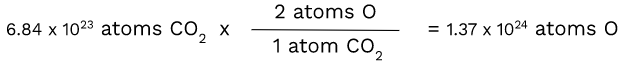
Since there are two atoms of O in one atom of CO2, we had to multiply by 2 to get the number of atoms of O.

You got this! Once you practice multiple problems involving dimensional analysis, it'll seem like a piece of cake. Sadly, these problems become more difficult as the course progresses but as always, practice makes perfect.