<< Hide Menu
9.6 Solving Motion Problems Using Parametric and Vector-Valued Functions
2 min read•june 18, 2024
9.6 Solving Motion Problems Using Parametric and Vector-Valued Functions
In this study guide, we are going to apply what you’ve learned about vector-valued and parametric functions to motion problems so you can take on anything the AP Calculus BC exam throws your way. From understanding the nuances of displacement and distance traveled to integrating vector-valued functions, you will develop the skills needed to solve complex motion problems. 🚗
🚘 Recap of Motion Terms
Before we dive into the problems, let’s refresh our memory on the definitions of position, velocity, acceleration, displacement, and distance traveled. If you want a more thorough review than the one provided below, we’ve got you covered.
📍Position
Position refers to the location of an object at any given time. It is a measure of where the object is situated within a coordinate system. In calculus, we denote a position function using .
🚄Velocity
Velocity is the rate of change of position with respect to time. In more straightforward terms, it tells us how fast an object is moving and in what direction. Mathematically, velocity is the derivative of position, denoted as , where represents the rate of change of position.
🚤Acceleration
Acceleration is the rate of change of velocity with respect to time. It describes how quickly the velocity of an object is changing. In mathematical terms, acceleration is the derivative of velocity, denoted as , where represents the rate of change of velocity.
Since acceleration is the derivative of the velocity, and the velocity is the derivative of the position, acceleration can also be defined as the second derivative of the position:
↔️Displacement
Displacement is a straightforward measure of the change in position of an object. It tells us how far the object has moved from its initial position to its final position, regardless of the path it took to get to its final position. Mathematically, it is represented as the following, where is the displacement, and and are the final and initial positions, respectively.
If you want to know how much ground an object has covered in total, look no further than its displacement.
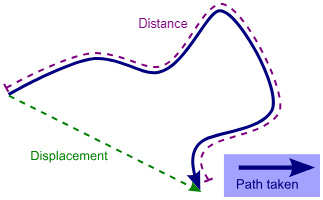
Image Courtesy of Wikipedia.
👟Distance Traveled
On the other hand, distance traveled is a measure of the total path length covered by an object. It accounts for the entire journey, regardless of the direction taken. Unlike displacement, which focuses on the change in position, distance traveled is concerned with the total ground covered.
To illustrate this concept, consider this analogy of forgetting your homework in the morning. If you leave your house, realize you forgot your homework, and return to get it, your displacement is zero because your final position is the same as your initial position, since you are still at your house.
However, your distance traveled is the sum of the distances covered during both trips, capturing the total ground you covered, even if you end up back where you started. If you traveled a mile before realizing you forgot your homework, then went back to get it, your distance traveled would be 1 mile + 1 mile = 2 miles, but your displacement would be zero.

Image courtesy of Pinterest.
↘️ Calculus with Vector-Valued Functions
A vector-valued function can be represented as , where and are functions that define the position of the object at time . The derivatives of these functions yield the velocity and acceleration vectors. We will now explore how to manipulate a vector-valued function in the context of motion problems.
Let's consider the position function . By taking the derivative of each component of this function with respect to time, we can determine the velocity vector. Taking the derivative, we obtain the velocity vector . From this equation, we can determine that the velocity in the x-direction is , and the velocity in the y-direction is .
Furthermore, to find the acceleration vector, we take the derivative of the velocity vector. For the given example, the acceleration vector is derived as . From this equation, we can conclude that the acceleration in the x-direction is a constant 2 units (usually ), and the acceleration in the y-direction is units.
Integrating to Find Displacement
Next, we’ll learn how to find the displacement of an object using calculus. Recall that the displacement is defined is the difference between the final and initial positions of an object, no matter what path it took. In calculus, we can take the definite integral of the velocity vector to obtain the displacement vector. Let’s use the velocity vector to find the displacement of an object from time to .
To find the displacement vector , integrate each component separately with respect to time:
We’ll finish up by evaluating these integrals:
The displacement vector is then given by . So, the displacement of the object from time to was 117 units in the positive x-direction and 21 units in the positive y-direction.
On a graph, the displacement can be determined by calculating the area under the curve of the velocity function, which is exactly what the definite integral of the velocity function accomplishes.
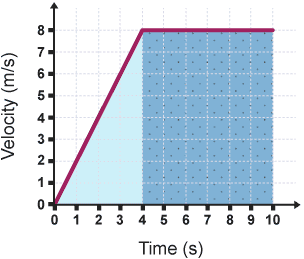
Image courtesy of Resourceaholic.
Using Arc Length to Find Distance Traveled
Recall that the distance traveled by an object is a measure of the total length of the path it took. In calculus, we can measure the distance traveled by finding the total length of the curve that represents the path of the object. And, you already know a way to find the total length of a curve: arc length! The arc length formula for vector-valued functions is
where is a vector-valued function. This formula tells us to take the definite integral of the magnitude of the derivative of the function. Whew, that was a lot in one sentence. Read it again to make sure you understand how the formula works. Check out a more detailed explanation of the arc length formula and how it relates to distance traveled if you’re a bit confused, and stay tuned for a walkthrough of a distance traveled problem.
🕓 Calculus with Parametric Functions
Many of the same concepts from above apply to parametric functions. In parametric functions, the parameter acts as a variable that varies over a specified domain, influencing the values of the associated functions. The general form of a parametric function is
where and are functions of . In parametric functions, each component of the vector is expressed as a separate function of time, offering a more detailed description of the motion of an object. The position functions and tell us that an object has a position on the x-axis that varies according to the function with respect to time, and a position on the y-axis that varies according to the function with respect to time. Let’s find the velocity and acceleration functions using this position function. To find the velocity functions, we take the derivative of each parametric function with respect to time:
To find the acceleration functions, we take the derivative of the velocity functions with respect to time:
Remember that each of these quantities tells us the rate at which that quantity is changing with respect to time, and in which direction (x or y).
Integrating Parametric Functions to Find Displacement
Just like we integrated the components of a vector-valued function to find the displacement of an object, we can integrate the x and y functions separately to find the displacement. Let’s take the functions and and find the displacement from to .
From these equations, we can tell that the object’s final x-position was 23 units to the left of its initial x-position, and its final y-position was units above its initial y-position.
Using Parametric Arc Length to Find Distance Traveled
The formula for parametric arc length is written a bit differently than the formula for the arc length of vector-valued functions, but you will soon realize that the two formulas are essentially the same. We won’t go into the details of how the formula is derived in this guide, but you can check out our guide on parametric arc length to learn more. The formula for parametric arc length is:
This may seem like a crazy formula, but if you read it one operation at a time, you can see that this formula is telling you to find the magnitude of the derivatives of a parametric equation.
✏️ Practice Problem
Try this out on your own before looking at the explanation to level-up your calculus skills!
A particle moves along a curve defined by the vector-valued function in meters. Determine the total distance traveled by the particle from second to seconds.
✅ Solution and Explanation
Since this is a distance traveled problem with a vector-valued function, we’ll use the formula to determine the answer. Working from the inside out, the formula first has us find the derivative of the position function (the velocity!). The derivative of is
Next, we need to find the magnitude of this derivative. Since this is a vector-valued function, and a vector has an and a component, we need to use the formula for the magnitude of a vector, which is derived from the Pythagorean Theorem. The formula is , and plugging in the x- and y-components of , we obtain .
But wait! 🛑 Think about what we just did. We took the derivative of the vector-valued function with respect to , giving us and , then found the magnitude of the derivative. Sound familiar? That’s because the arc length formula for vector-valued functions and the arc length formula for parametric functions is one and the same!
Okay, back to the problem. Now that we have the magnitude of the derivative, , we need to take the definite integral from to seconds. The integral setup looks like this:
where is the arc length, or in this case, distance traveled. Using a calculator to solve the integral, we get approximately 0.003 meters.
📕 Conclusion
Whew, that was a lot! Great job for pushing through and learning all about motion problems that use parametric and vector-valued functions. We started by revisiting fundamental notions of position, velocity, and acceleration, emphasizing their interconnectedness through differentiation. We also calculated displacement and distance traveled, and showed how the two quantities were different.
Now that you know all about how to solve motion problems using parametric and vector-valued functions, you’re ready to crush your AP Calculus BC exam! 🤩

© 2024 Fiveable Inc. All rights reserved.