<< Hide Menu
8.11 Volume with Washer Method: Revolving Around the x- or y-Axis
5 min read•june 18, 2024
8.11 Volume with Washer Method: Revolving Around the x- or y-Axis
Welcome back! For this section, brush up on the basics by covering the disc method here in section 8.9 and the disk method with different axes here in section 8.10. This topic almost always appears as part of an free-response question (FRQ), so study up!
🛁 The Washer Method
Remember the general integral format from 8.10 Volume with Disc Method: Revolving Around Other Axes? You’ll need to expand it for the washer method!
So what is a washer?? Very simply, it’s a circle with another circle cut out of it in the middle.
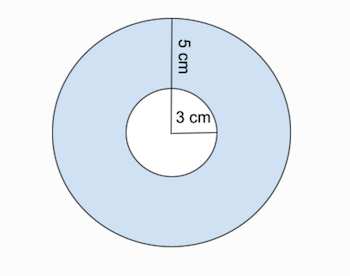
Image courtesy of study.com
Instead of circular cross-sections to calculate an integral, we use washer cross sections when given more than one function to rotate around an axis. A washer’s area can be calculated through the equation , where is larger than . By replacing the circle area equation () in the disc method with the washer area equation, we find the final washer method integral of:
where is the equation with the larger radius and is the equation with the smaller radius. Remember that is equal to the distance between the axis and function, which represents the radius.
The axis of rotation is , the lower bound is and the upper bound is . Also, on a graph, should be farther from the axis of rotation than in the specified interval.
Additionally, don’t forget that you need to square the functions and before subtracting from . For example, imagine that a washer had an outer radius of 4 and an inner radius of 2. The total area would equal instead of .
✏️ Solving with The Washer Equation
The general washer equation below works with any washer problem. So, how do you use it?
While you are always given at least 2 functions and told the axis of rotation when solving a washer problem, you usually have to determine the upper and lower bounds and figure out which function is or in the equation above. Let’s use a simple example!
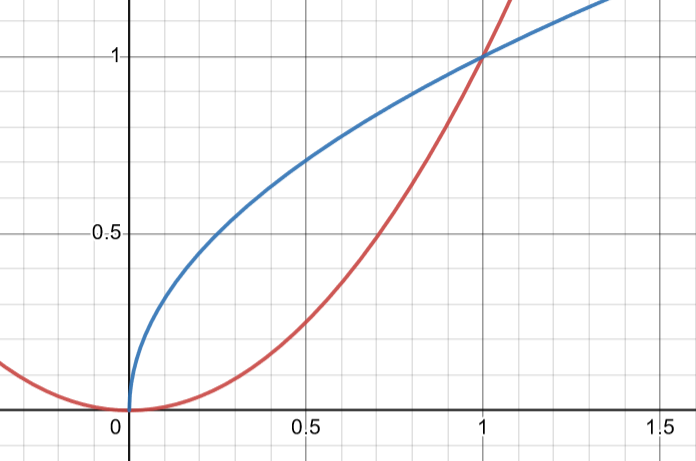
Graph created with Desmos
Imagine we want to find the volume of the solid created when the region bounded or enclosed by the functions and is rotated around the x-axis.
First of all, we need to determine our lower and upper bounds, represented by c and d in the integral equation. Although we aren’t directly given them in the problem, these bounds or limitations clearly occur where the 2 functions intersect. To find these, just set so and , which occurs at 0 and 1. You can also use a graphing calculator on the AP exam to find these intersections for you! In addition, using the formula that is the axis of rotation, we know that since we are rotating around the x-axis.
Next, we need to determine which of the functions is and which is . Visually, the blue function of is farther from the x-axis that over the lower to upper bound interval so and .
Drawing or graphing out each equation and the axis of rotation is very important as it allows you to identify the area to be rotated, estimate lower and upper bounds, and see which equation is farther from the axis of rotation.
This also keeps you from making common mistakes like wrongly assigning and . Don’t assume that the top function is always ! In the example above, if the axis of rotation was , then since it would be the function farther from the axis of rotation.
➕ Summing Up The Washer Method
To recap, we determined that , , , and . Plugging this information into the main integral equation gives:
This equation can also be simplified to:
Using the power rule of integration, this integral is equivalent to
Solving this out gives:
Make sure that your final answer is positive since volume is always positive! If it’s negative, recheck which functions you defined as and !
🤔 The Washer Method: Practice Question
Give the following question a try yourself before you see how we walk through it!
Find the integral that represents volume of a solid composed of the region bounded by and rotated about the line , where .
Here’s a list of what you need to identify in order to solve this problem:
- B value (axis of rotation)
- C and D values (Upper and lower bounds)
- and (Functions farther and nearer to the axis of rotation)
💭 The Washer Method: Solution
The best way to start your approach is by graphing the given functions and axis of rotation!
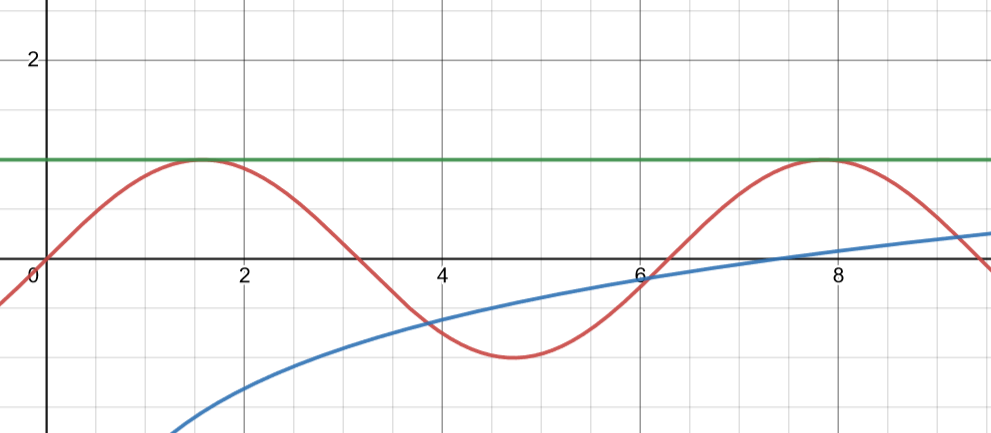
Graph created with Desmos.
Using the formula that axis of rotation is , we know that in our integral.
Next, we need to find the upper and lower bounds of our integral. By reading the problem, we know that x is stated to be less than 7, which is helpful as it identifies the specific area to rotate around the axis. As seen in the graph, this area starts at the intersection of the 2 functions at about and ends at the intersection where . Like some AP questions, this is impossible to find purely algebraically, so don’t forget your calculator!
There’s another intersection at , but we are ignoring it since this section breaks the given condition of
After finding the bounds, we need to determine which function is f(x) and which is g(x). Since the red function, or is farther from the green line, or axis of rotation, than the blue line, or , is and is .
Plugging everything into the general integral equation, we get:
Solving this integral isn’t possible using AP Calculus AB skills, but it is possible to take the integral of and using solving by parts, which are AP Calculus BC techniques covered here.
Plugging this integral into a calculator would give an answer of approximately 8.54.
To try to stump you, many questions on the AP exam involve functions that can’t be derived or integrated with the basic rules taught in class. Instead, these questions rely on your ability to identify different parts of the general revolution integral and how to relate to each other.
📒 Closing Out
The best way you can help yourself with rotation or 3D integral problems of any shape is by drawing or graphing each function! Remember that the steps for these problems are draw, identify, plug into an equation, and solve!
As long as you can identify the following, you should be mostly set for the test.
- B value (axis of rotation)
- C and D values (Upper and lower bounds)
- and (Functions farther and nearer to the axis of rotation)
Here’s another copy of the general washer equation in case you need it.
Remember to practice, practice, practice! 💪🏼

© 2024 Fiveable Inc. All rights reserved.