<< Hide Menu
5.12 Exploring Behaviors of Implicit Relations
6 min read•june 18, 2024
5.12 Exploring Behaviors of Implicit Relations
Welcome to the last key topic of unit five! We know that a function's derivative can be used to understand the behavior of a function. This holds true for implicit functions too!
🧠 Understanding Implicit Functions
An implicit function is a type of function that is not defined in the usual manner! Before this unit, you would see explicit functions that pass the vertical line test and take the form of:
In contrast, an implicit function is represented by an equation that has multiple variables on the same side of an equation. Although they look different and sometimes don’t pass the vertical line test, you can still determine the behavior of an implicit function using its derivatives.
Here’s an example of an implicit function:
Remember that implicit differentiation allows us to work with functions defined implicitly by taking d/dx of both sides of the equation to find dy/dx, which is usually defined in terms of both x and y.
🥇 First Derivative Applications of Implicit Functions
🎯 Critical Points on Implicit Functions
If you need a refresher on critical points, click here! In summary, all you have to do is to take the first derivative and determine when it is 0 or undetermined to find potential critical points. These points represent potential minima/maxima.
🪜 Steps To Find Critical Points on Implicit Relations
- Differentiate both sides of the implicit equation with respect to x or take .
- Solve for . This will give you the derivative of the function in implicit form.
- Set to identify any potential critical points. In addition, determine where is undefined
- Make a conclusion about each critical point by determining how changes signs around that point.
🧠 Behavior of Implicit Functions Using First Derivative
Let’s quickly recap how to analyze a function, since the rules apply for an implicit function as well!
- If is positive, then the graph of is increasing.
- If is negative, then the graph of is decreasing.
- If is increasing or has a positive slope, then the graph of is concave up.
- If is decreasing or has a negative slope, then the graph of is concave down.
- If changes from positive to negative at , then has a relative maximum at .
- If changes from negative to positive at , then has a relative minimum at .
Remember that for implicit functions, relative minimums and relative maximums may not be as intuitive to find when compared with viewing explicit functions!
🥈 Second Derivative Applications of Implicit Functions
After finding the first derivative implicitly, differentiate again with respect to x to find the second derivative. Be aware that the second derivative may involve , , and .
Once you have the second derivative, you can use the second derivative test to determine the concavity of the function and identify the points of inflection.
Here’s a quick recap regarding how to use the second derivative to determine the behavior of a function:
- If is positive, then the function is concave up.
- If is negative, then the function is concave down.
- A point of inflection is a point where changes concavity and . Make sure to check that is changing signs at this point by finding the value of just before and after the potential inflection point!
To review how to determine concavity, check out 5.6 Determining Concavity.
🧩 Behavior of Implicit Functions: Practice Problems
Now that we know how to interpret the behavior of implicit functions, we can do some practice!
Practice Problem 1
Consider the implicit equation Find the critical points and determine their nature (local minimum, maximum, or neither).
When you do the implicit differentiation, you should get:
Solve for !
We now have the first derivative! Find the critical points by setting and solving for x.
The original equation was so if , and , so 2 potential critical points are and .
Also, don’t forget to set undefined and solve! This function is undefined when the denominator is 0, or when . Plug back in to find out the x values for these critical points.
First Derivative Test Chart
Now you can take your 4 critical points and make a conclusion about the behavior of the function around those points.
| The Point | Dy/Dx To the Left | Dy/Dx To The Right | Conclusion |
| + | - | Maxima | |
| - | + | Minima | |
| + OR - | + OR - | Undefined | |
| + OR - | + OR - | Undefined |
Why are two of the critical points undefined as maxima or minima? Let’s look at a graph of the function to see!
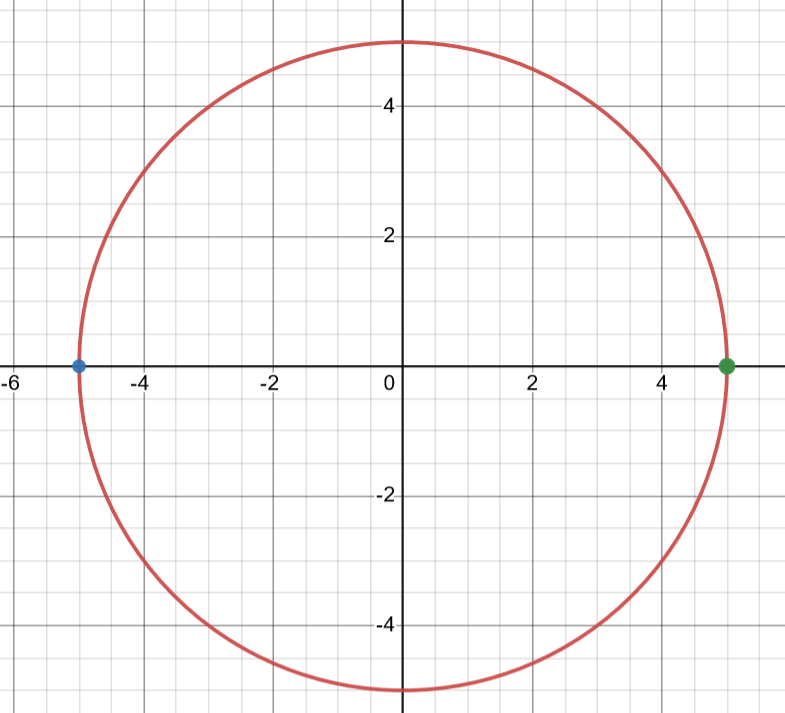
Courtesy of Desmos
As you can see here, below the critical point of , the function has a negative slope or negative derivative in the 3rd quadrant of the graph. Above the same critical point, in the 2nd quadrant, the function has a positive slope and derivative. The critical point has similar changes in the derivative sign from positive in the fourth quadrant to negative in the first quadrant.
However, despite this change in sign, these points are not conclusively maxima or minima under the definitions of Calculus AB. This is because to find maxima and minima, we need our critical points to either be endpoints of explicit functions or be in the “middle” or an implicit function (have valid points with x values greater and less than the critical point).
Here, there are no points to the left of (-5,0) and no points to the right of (5,0). Due to the function’s implicit nature, this makes it difficult to determine whether either point is a minimum or a maximum.
Phew! You made it through this question. 😎
Practice Problem 2
A ladder is leaning against a wall. The bottom of the ladder is sliding away from the wall at a constant rate of 2 ft/s. If the ladder is 10 feet long and its bottom is originally 6 feet away from the wall, how fast is the top of the ladder sliding down the wall when the bottom is 8 feet away from the wall?
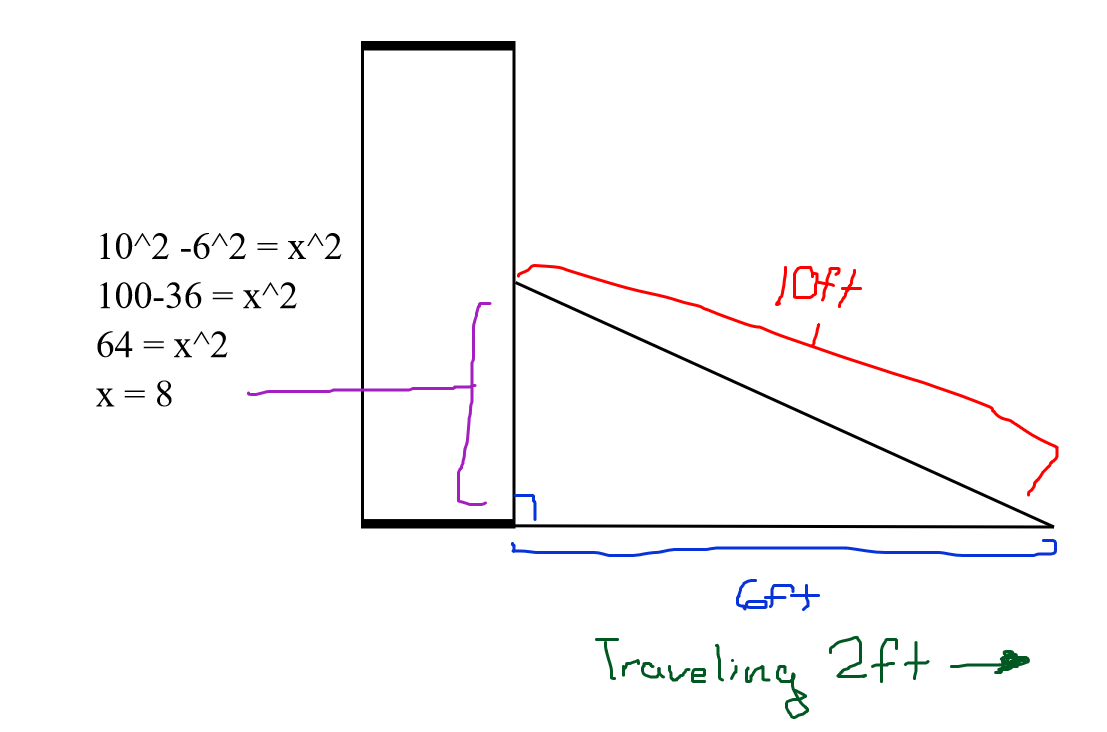
Courtesy of Author
First, let’s list out the given information!
- Horizontal rate of change of the bottom of the ladder = 2 ft/sec.
- Length of the ladder = 10 ft.
- Distance from the wall = 6 ft.
- What to Find: Vertical rate of change of top of the ladder when the distance from the wall is 8ft
Next, we need to make an implicit equation that represents the ladder. We will use x for the ladder’s horizontal distance from the wall and y for its vertical distance from the ground. Combining this with the Pythagorean Theorem, we get
Use implicit differentiation to get
Solve for to get
Don’t stop here! Instead of finding the change of y with respect to x, or , we instead want to find the change in y with respect to time, or .
To do this, we will be using the Chain Rule that states the following:
You can also look at this algebraically to see that the dx factor in the numerator and denominator cancel to give us .
In the problem, we are given the information that , throughout the entire ladder’s movement (constant rate).
Substitute this value into the chain rule, to find the final equation:
Now, we need to substitute x and y, from our target scenario, when the bottom of the ladder is 8 feet away from the wall. To find this, use the Pythagorean Theorem.
- x = 8 (distance from the wall)
- y = ? (height of the ladder)
- Solve for y:
Plugging the values of y = 6 and x = 8 into our earlier equation gives us
Therefore, the top of the ladder is sliding down the wall at a rate of when the bottom is 8 feet away from the wall.
Remember that the directions up and right are considered positive while directions down and left are considered negative. Since is negative, the ladder is sliding down and it’s vertical distance from the floor is increasing.
Pat yourself on the back for getting through another practice problem! 🥳
⭐️ Conclusion
To solve any implicit differentiation problem, follow these simple steps!
- List out any information given and write down your final goal.
- Draw a picture of your scenario or graph the equation given.
- Make an equation to represent the situation given. Some problems give this formula to you while others require you to use basic mathematical models such as the Pythagorean Theorem.
- Use implicit differentiation in your equation.
- Either find critical points by setting or use the chain rule with earlier information to find or .
- Check your critical points using minima/maxima tests or plugin earlier information into the equation given by the Chain Rule.
- Double-check your work, making sure any positive/negative signs make logical sense.
Now you’ll be able to work through problems where you have to use a function’s or implicit function’s derivative to understand the behaviors the function. Great job and see you in the next guide! 👋🏽

© 2024 Fiveable Inc. All rights reserved.