1.13 Removing Discontinuities

1.13 Removing Discontinuities

In this guide, we’ll be diving into the fascinating world of discontinuities. Ever looked at a graph and noticed it suddenly jumps or has holes? These are discontinuities, and sometimes, we can remove them. Let's explore how we can smooth out these mathematical speed bumps and make our functions continuous.

⭕ What are Discontinuities?

Before we patch things up, let's first understand what we're dealing with. Discontinuities occur where a function "breaks." There are three types: removable, jump, and infinite. Today, we are going to focus on removable discontinuities.

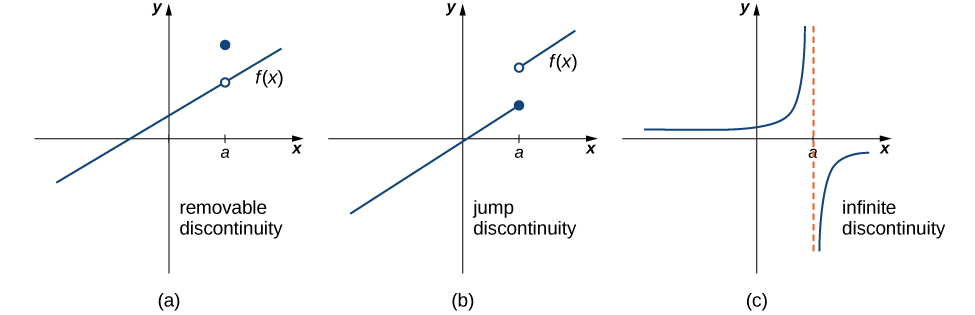
Image courtesy of LibreTexts Mathematics

---

📍Removable Discontinuities

Removable discontinuities are also sometimes called “holes” in a graph. They exist when a function is undefined at a point, but its limit exists. We can fill this hole to make the graph continuous. Here’s an example:

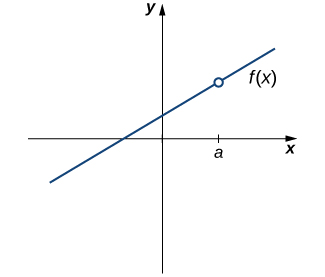
Image courtesy of LibreTexts Mathematics

We can see in this graph, the limit as $x$ approaches $a$ exists, it’s just undefined at that point. But, if we color in the circle (in other words, remove the discontinuity), the graph will be continuous over the interval in the image.

🌀 Filling the Gap

To remove a discontinuity, we redefine the function's value at that point to equal the limit of the function as x approaches that point. For example:

To remove this discontinuity, we can factor the denominator and cancel like terms, like so:

This function no longer has a discontinuity at $x=1$, instead, it is defined as $\frac{1}{2}$.

✏️ Practice Filling the Gap

Consider the function $g(x)$ defined as follows:

where $k$ is a constant. Determine the value of $k$ that would make $g(x)$ continuous at $x = 1$.

Here’s the solution! ⬇️

First, we need to factor our numerator. This will allow us to see whether we can cancel out the denominator, which is what is causing our discontinuity.

We see that there is an $x-1$ term in our numerator, so we can cancel it with the $x-1$ in the denominator!

For $x=1$,

---

📈 Piecewise Functions

For piecewise functions, we can ensure continuity by checking the right and left limit of the function, and assuring that the value is the same as the one defined at the point.

✔️ Ensuring Continuity

Consider $f(x)$ defined by two pieces of a function on either side of $x = a$:

• On the left side, $f(x)$ approaches $L$ as $x$ approaches $a$.
• On the right side, $f(x)$ approaches $M$ as $x$ approaches $a$.

For $f(x)$ to be continuous at $x = a$, we need $L = M = f(a)$.

For example, this image depicts the continuous, piecewise function

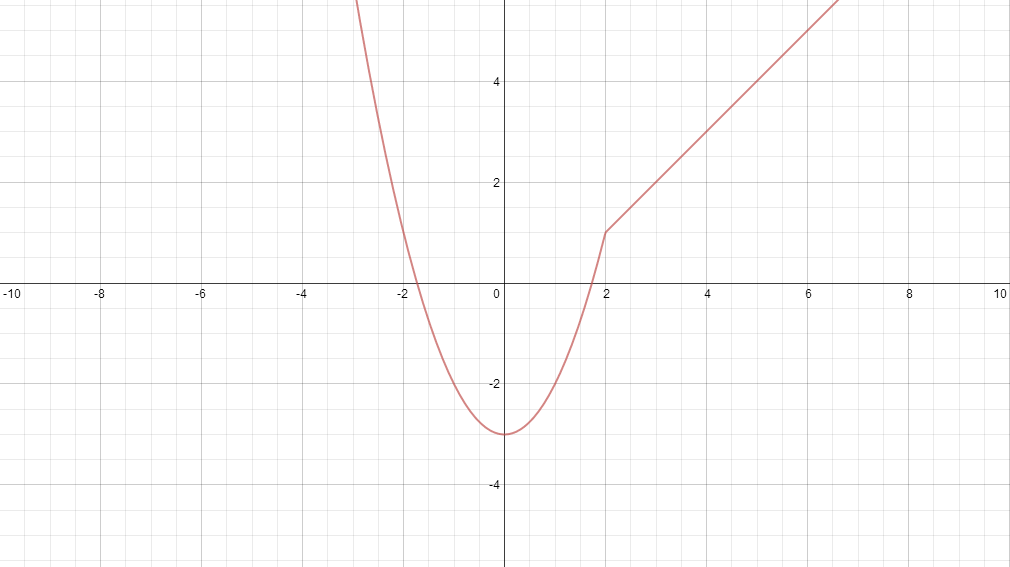
Image courtesy of mathcoachblog

We can see the the limit of $f(x)$ as it approaches the point $a=2$ from the left is equal to $1$, and similarly, from the right, it is also $1$. Finally, $f(x)$ is defined at $a=2$ as $1$. Thus, our function is continuous.

✏️ Practice Ensuring Continuity

Consider the function,

What must $a$ be set to for the function to be continuous?

To solve this problem, we will use the first part of the piecewise function to solve for $a$ at $x=2$. First, let’s factor and cancel some terms:

Now, let’s plug in $x=2$:

Finally, we set this equal to $a$ and solve:

---

📷 Visualizing Continuity

Graphs are an excellent way to see continuity (or the lack thereof). Use graphing tools to visualize the function and identify discontinuities. A continuous graph can be drawn without lifting your pencil!

✏️ Practice Visualizing Continuity

Graph the function $f(x)=\frac{x^2-9}{x+3}$ over the interval $[-5,5]$. Is it continuous? Can you make it continuous?

The graph of this function looks like so:

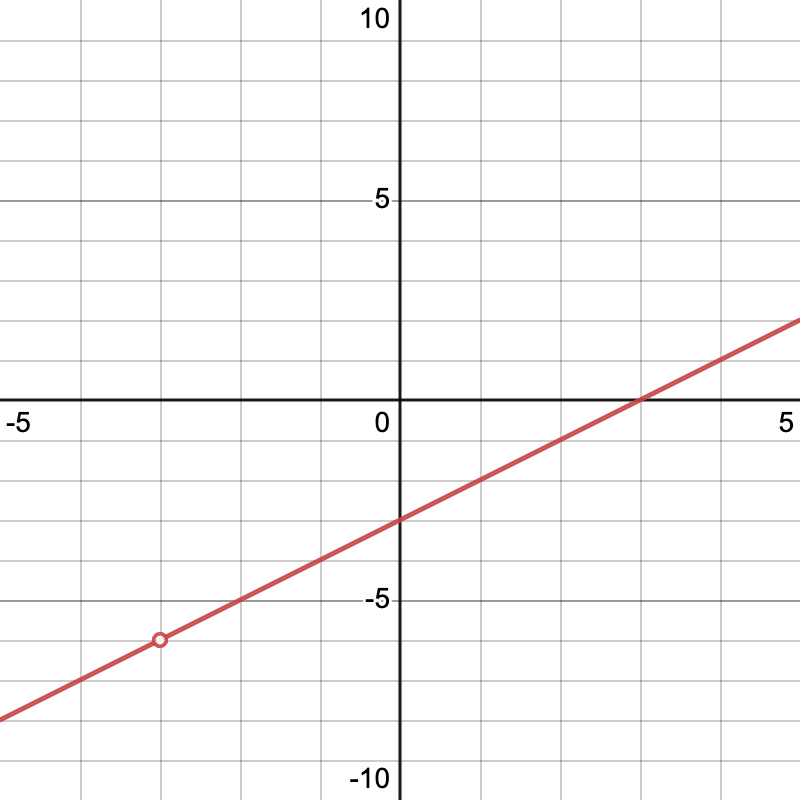
Image courtesy of Emery

You can see that there is a discontinuity at $x=-3$. But, we can remove it by factoring!

Plugging in $x=-3$, we find that $f(x)=-6$ at $x=-3$, making our function continuous.

---

⭐ Closing

📚 AP Calc is practice-driven! Attempt more problems, especially from past AP exams, to strengthen your understanding. Always check for continuity and practice "patching up" those functions. Great work! 👏