1.10 Exploring Types of Discontinuities

1.10 Exploring Types of Discontinuities

Now that we covered limits and continuity, let’s get into discontinuities! ⬇️

Introduction to Discontinuities

To describe what a discontinuity is we should know what continuity is. For a function to be continuous it must be:

1. defined for all of x.
2. must have a defined limit at all points.
3. must have matching limits approaching from both sides of the point.

Some of these may be confusing to picture, but it may be easier to picture when it doesn’t happen, introducing discontinuities. A discontinuity is any point in the domain at which the function is no longer continuous. More simply, if you’re drawing the graph of a function and have to lift up your pencil to get to the next point, that’s a discontinuity. ✏️

Removable Discontinuities

Removable discontinuities are often the most simple—these discontinuities occur when a single point from the graph is discontinuous. These are also known as holes.

There can be two reasons for a removable discontinuity. The first is a “blip” in the function, often seen as an inequality. The second is a common factor in a fraction function.

Example of a Removable Discontinuity

Try and draw the piecewise function:

Your function should look like this!

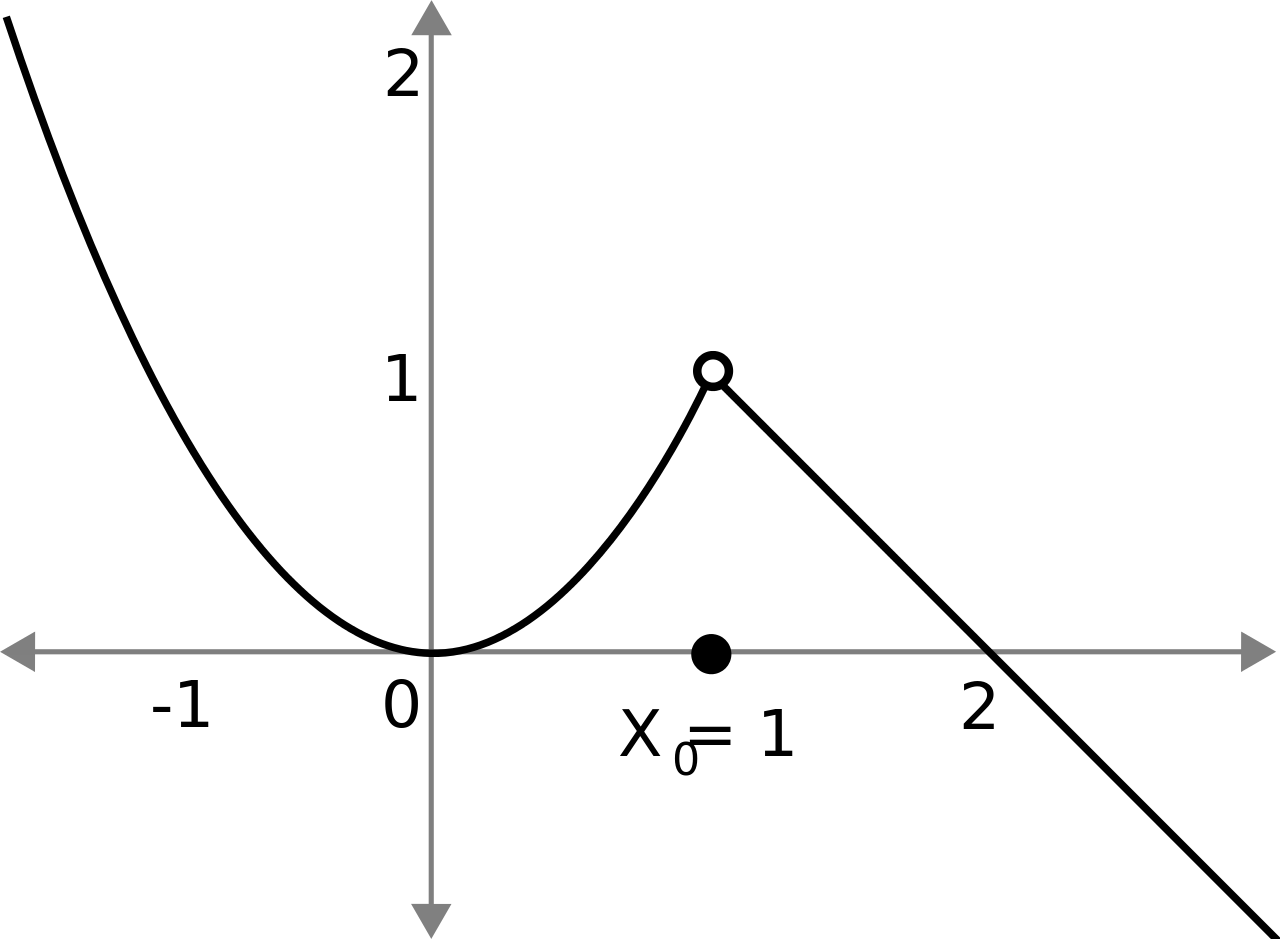
Image courtesy of Wikipedia

In this example, the function is not defined at $x = 1$ because the point is far off from the line, requiring you to lift up your pencil to put in that dot!

Example of a Common Factor Discontinuity

Try graphing the piecewise function:

Your function should look like this!

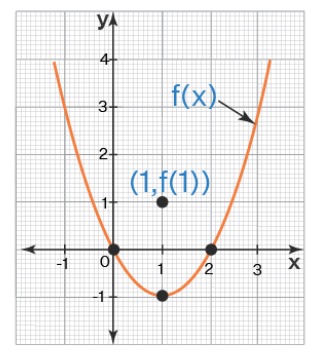
Image courtesy of cuemath

The graph looks like this because an $(x-1)$ factors out from the numerator and the denominator leaving $y = x^2 -2x$ and a removable discontinuity at $x = 1$. While $x-1$ is factored out from the equation, in the original when $x=1$ you get a result of $0/0$, an undefined point. Luckily, in this case, the function is defined separately by the piecewise function, but it is still a discontinuous graph.

Jump Discontinuity

Jump discontinuities are when there is a vertical “jump” between sides in a graph. This will look like a line suddenly shifted up or down, like a trench! This can be found mathematically when the limit from the left side does not equal the limit from the right side.

Example of a Jump Discontinuity

Let’s try to graph another piecewise function:

Your graph should look like this!

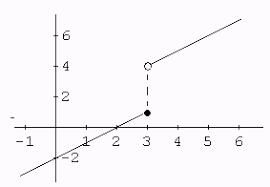
Image courtesy of byjus

The vertical jump up three units on the y-axis defines this as a jump discontinuity!

Asymptote Discontinuity

An asymptote discontinuity is when the limits of the left side and right side of the equation approach infinity, either negative or positive. They can even be in the same direction! Like a game of Chicken, the two functions approach each other on the x-axis and up or down swerve at the last second!

Example of an Asymptote Discontinuity

Let’s try and graph something a little more simple than a piecewise function. Draw a simple graph of the equation $y = 1/x$.

Your graph should look like this!

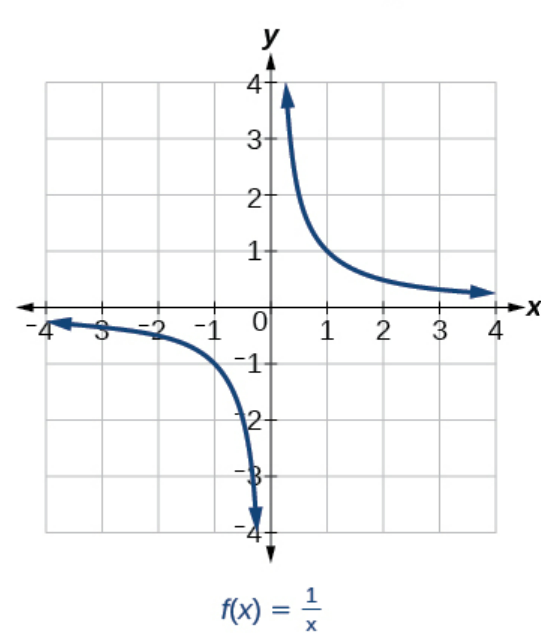
Image courtesy of math libre

---

Recap: How to Identify Discontinuities

Removable Discontinuities

• A single dot away from the graph
• A factored function
• Limit at a point does not exist

Jump Discontinuities

• The limit from the right does not equal the limit from the left
• The lines don’t match up

Asymptote Discontinuities

• The limit goes to infinity
• There are two lines that point straight up or down

Remember, practice makes perfect when exploring and identifying these discontinuities. Good luck! 🍀