1.6 Determining Limits Using Algebraic Manipulation

1.6 Determining Limits Using Algebraic Manipulation

Algebra’s amazing! When working with limits, we can use algebraic tools like factoring, conjugates of sums or differences, and alternate forms of trigonometric functions to make things easier on our end. 🙃

✏️ Factoring

Remember factoring?! Factoring in math means breaking down an algebraic expression into simpler, more manageable parts. It involves finding the factors (numbers or other expressions) that, when multiplied together, give the original expression.

For example, if you have an algebraic expression 2x + 4, you’ll notice that 2 goes into both terms, so we can pull it out and get 2(x + 2)! To check if you’re correct, you can redistribute the 2 into both terms and get 2x + 4 once again. Yay! 🎇

Let’s try a couple of problems:

🚆 Example Set 1: Factor Away!

Example Set 1: Question 1

Find the following limit:

Now, the easy way out is to plug 3 into the equation, so, $3³ - 3² - 3 = 27 - 9 - 3 = 15$, which is fine in this case…but what if we have a huge number that’s hard to solve in your head? In that case, you’d want to break down the algebraic equation to make life as easy for you as possible. That being said, what do you notice in the expression? 🧐

x goes into all of them! In other words, we can factor x out. Doing so leaves us with $x(x^2 - x - 1)$. Now we can plug in 3 to get $3 (3² - 3 - 1) = 3 (9 - 3 - 1) = 3 (5) = 15$.

Isn’t that easier to work with than directly plugging in 3 at the beginning of the equation? That’s the goal of factoring as a strategy.

Example Set 1: Question 2

Let’s try another example:

Again, let’s look for patterns! Can we pattern something out? Hmmm… maybe $x²$? Yep! Factoring it out gives us.

Seems like we can’t break it further down. Let’s plug -1 in.

And we get (1) (-3/3) = -1. Not too bad, huh? Let’s spice things up with our next example.

Example Set 1: Question 3

It looks intimidating, but again, the key is to break things down. If you want a refresher on factoring, Fiveable’s Factoring Polynomials study guide will be your best friend. In this case, let’s factor both parts of the algebraic expression.

• For our numerator, which two numbers add up to -5 and has a product of -6? 1 and -6. (-3 and -2 won’t work because their product is +6 even though they add up to -5; -1 and 6 won’t work either because they add up to +5 even though their product is -6. We’ll use this same logic for the denominator.)
• For our denominator, which two numbers add up to -7 and has a product of 6? -1 and -6.

So, our factored expression now looks like this:

Can we make this expression simpler? Can we cancel something out? Perhaps (x - 6)? Getting rid of x - 6 leaves us with…

Plugging in 1 gives us 2 / 0, which means the limit does not exist (we can’t divide a number by 0).

Feel comfortable enough? Unfortunately (or fortunately if you hate the idea of factoring), not every problem will be factorable and may have more icky components like radicals (i.e. square roots); in that case, another strategy may be more appropriate to use. Allow me to introduce another friend ⬇️

---

🎈Rationalizing Denominators Using Algebraic Conjugates

Sometimes, you’ll encounter terms with square roots at the denominator of a fraction. That’s not ideal especially when it has variables like x. To “get rid” of that square root, we can multiply the whole term with the radical by its conjugate, the same exact term but with a different sign in the middle. For example, the conjugate of (a + b) is (a - b). The following terms below, as another example, are conjugates of each other.

This works especially if the initial plug-and-chug method gives us an indeterminate (0 / 0) answer. Let’s work on a couple of examples:

🤔 Example Set 2: Let’s Be Rational Here…

Example Set 2: Question 1

If we just plugged in x = 5 right away, we’ll get -16 / 0… which doesn’t work out. The alarm bells in your head should be screaming “there’s a radical!” In that case, we’d want to rationalize the denominator to get rid of the radical downstairs by multiplying the numerator and the denominator by the conjugate term:

Let’s multiply the terms out via the FOIL method:

Simplify…

Good news: we can cancel out (x - 21)!

Plugging in x = 5: sqrt(9) + 5 = 3 + 5 = 8! Woo-hoo!

Example Set 2: Question 2

In our next example, the radical starts at the numerator. For the rationalization via conjugate method, the radical doesn’t have to strictly be in the numerator or denominator. One way to check is to plug in the number in the beginning to see if you get an indeterminate answer; then, you can proceed with rationalizing the expression.

Plugging in 9 to x gives us 0 / 0. Bad! Let’s rationalize:

Simplify (aka cancel out common terms), then plug in!

---

📐 Alternate Forms of Trigonometric Functions

One last thing: what if neither factoring nor rationalizing functions work in simplifying our limit expression but we’re stuck with an indeterminate answer? If the expression involves a trigonometric function (sin, cos, tan, etc.), then you’ll most likely have to use an alternate form of said function.

On the AP Exam, you’ll be expected to recall the limits of common trigonometric functions. Below are the most common formulas you’ll be expected to remember. 📏

🤠 The (Trig) Laws of the Land

Rule #1:

Rule #2:

Rule #3:

Rule #4:

To better understand these formulas, let’s discuss them individually.

Rules #1 and #2: These two rules are pretty much the same as what we would do for any limit. The first way to solve a limit is to plug in the x value into the function. In the formulas above, the value “c” is being plugged in to try and determine the limit. If you are asked to find the limit of sin(x) as x approaches 1, then you simply plug in 1 and get your answer.

Rule #3: This rule is VERY common in AP Calculus. Moving forward, you should be on the lookout for this rule.

Rule #4: This last rule is not as common as rule #3 but it's still just as important. To understand this rule better, check out the second example below.

☘️ Example Set 3: Magic Trig-cks!

Example Set 3: Question 1

Let’s compare this to our mini-rulebook above. It seems like this problem is similar to that of Rule #3 with a slight change. To use Rule #3, we need the inside term in sin(inside term) / denominator term = denominator term to be similar so that they equal 1. Right now, however, the inside term (which is 4x) is not equal to the denominator term (which is x)!

To fix that, let’s multiply both numerator and denominator by 4. Then, we can use Rule #3 for sin(4x)/4x since we know that expression is equal to 1. We can then find the limit from there.

Feel better? Let’s keep going and ingrain the trig rules into your head.

Example Set 3: Question 2

That being said, next up is a practice problem on Rule #4!

Recap: sec(x) = 1/(cos(x))! Thus, you can use the following steps to solve the limit. In words, once you use this identity, multiple both numerator and denominator by cos(x). Then, you can separate the terms: plug 0 into the left term (cos(0) = 1) and use Rule #4 on the right term.

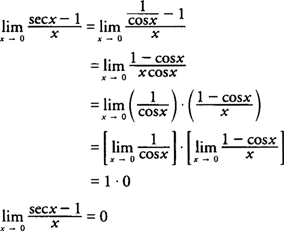
Image courtesy of Anusha Tekumulla

Example Set 3: Question 3

Let’s make things more interesting with some twists and turns:

Hmm, now there’s sin(inside terms) on both numerator and denominator…which looks confusing. What we can do is to rewrite the expression to separate the numerator and denominator into two factors:

Then, we can stitch the pieces relevant to Rule #3 together:

Further simplify!

All three methods of algebraic manipulation to determine limits may seem scary to deal with at first, but with practice, you’ll get the hang of it and be more effective in solving similar problems in the future. Good luck! ☘️