<< Hide Menu
1.15 Connecting Limits at Infinity and Horizontal Asymptotes
5 min read•june 18, 2024
1.15 Connecting Limits at Infinity and Horizontal Asymptotes
Remember infinite limits from the last study guide? We’re back to that, but this time we’re connecting these limits to horizontal asymptotes.
🔍 Review: Limits to Infinity
What happens to a function as a variable gets very small or very large? We say that this variable is “approaching negative infinity or infinity.” By finding the limit as x approaches infinity, we are trying to find what the y value is approaching as the x value continues to increase.
🧐 Finding Limits to Infinity
So, how do you find the limit as x approaches infinity or negative infinity? You need to find the horizontal asymptote!
🚥 Horizontal Asymptotes
A horizontal asymptote is a y value that the graph cannot touch. 🛑 The function will continue to get closer to the horizontal asymptote but will never touch or cross it. Let’s look at an example:
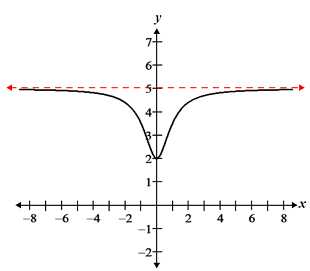
Image Courtesy of MATH.net
On the graph, there is a horizontal asymptote at y = 5. The function cannot cross the graph at that point. Therefore, .
🔍 Finding Horizontal Asymptotes
There are a few rules to follow when finding the horizontal asymptote (and in turn, the limit at infinity) of a function. In order to apply the rules, think of a function as .
🥇 If the degree of p(x) < the degree of q(x), then the HA (Horizontal Asymptote) = 0.
🥈 If the degree of p(x) > the degree of q(x), then there is no horizontal asymptote.
🥉 If the degree of p(x) = the degree of q(x), then the HA is the ratio of the coefficients.
Finding the HA can be used to find the limit when the function is indeterminate, meaning that you have . There are also some other ways to find limits approaching infinity.
Exceptions to These Rules
- The limit of an oscillating function at infinity does not exist.
- Ex:
- Any function that is part of the squeeze theorem will equal 0 as it approaches infinity.
- Ex:
🌱 The Growth Rates of Functions
It is important to note that not all functions grow, 🪴 or increase, at the same rate. The order of the growth rates of common functions is as follows, from slowest to fastest:
- log < root < polynomial < exponential.
Knowing the growth rates of each function can be helpful when determining its limit at infinity.
✏️ Infinite Limits & Horizontal Asymptotes Practice
Infinite Limits: Example 1
Evaluate the following limit:
On the bottom of the fraction there is an exponential function, . Since we know that exponential functions have very high growth rates, the denominator of the function will get increasingly larger, while the numerator will stay relatively small. Therefore it is like we have a .
Since the number on the denominator is so much larger than the number in the numerator, when divided, the quotient = 0. Therefore .
Infinite Limits: Example 2
Evaluate the following limit:
In this problem, since the exponential function is in the numerator, we have a . Therefore, . When you have a function that grows to be so large, so fast, all the other numbers are negligible comparatively!

© 2024 Fiveable Inc. All rights reserved.